Emergence of urban growth patterns from human mobility behavior

城市自下向上的增长方式导致了用标度律描述的碎形/分形(fractal-like)城市结构。相关渗流模型(percolation model)
通过施加强空间相关性成功建模出城市的几何形状(urban geometries)。然而,在空间相关的城市增长背后的潜在机制的起源仍然很大程度未知。
本文介绍了一个计算城市增长模型,在人类移动行为的微观基础上捕捉城市增长的空间相关性。本文将提出的模型与三个实证数据集进行对比,发现人类移动中强社会联系和长时记忆是碎形城市形态的两个基本原则,以及三个重要的三个城市增长的定律。该模型联系了城市增长模式的实证发现与人类移动行为。
Intro
曾有研究学者提出,由于旨在优化城市发展中城市功能和空间利用的可达性的自上向下严格的城市规划规定,城市应该具有对称和规则的形态。
然而,越来越多的城市数据表明,城市是以自下而上的方式发展的,需要理解其微观基础。
发现三条基本的实证定律:
- 城市大小的分布符合指数在-2.0左右的标度律
- 城市人口随区域面积超线性增长
- 城市占据区域随距城市中心径向距离指数递减
相关渗流模型的重要发现是在城市增长中需要强烈的空间相关性来再现标度关系。
所以研究人员提出把城市增长分为两个方面进行建模:新簇的出现和存在簇的增长。
先前的模型虽然成功解释了城市形态,但都把城市增长建模为物理粒子的随机过程,遗留了人类移动在微观基础上很大程度未知的问题。
Results
Human movement models
现存的人类移动模型基于社会联系和长时记忆可以被分为四类。
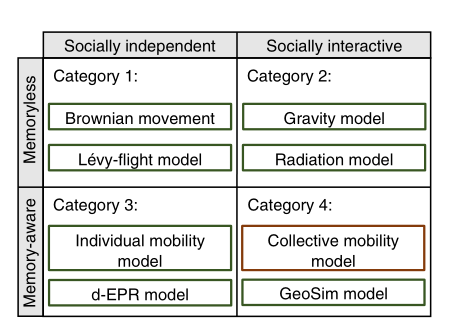
社会联系指个体的移动会影响其他人。
长时记忆指个体未来的移动行为受他历史移动的影响。
(1)Catergory-1
Category-1将人类移动看作没有社会联系的粒子随机移动。
布朗运动中个体的位移正态分布,与物理粒子不同,实证数据中人类移动符合胖尾分布(幂律)。
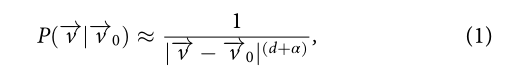
转移概率随距离(即移动花费的距离)减少,即大部分时间人们短距离移动,偶尔长距离移动。
忽略社会关系和长时记忆,该式表明人类移动遵循莱维飞行模型,但莱维飞行和布朗运动在时间t接近无穷时都预测均匀的人口分布,与实证观测相反。
(2)Catergory-2
Category-2中辐射模型和引力模型都起源于对迁移的研究,两地之间的移动流取决于他们的人口。
引力模型的转移概率如下
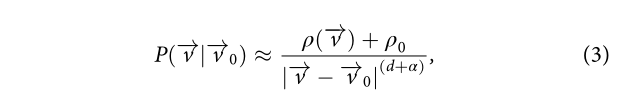
其中
但是引力模型遵循与莱维飞行相同的扩散过程,在t很大值下预测均匀的城市人口分布。
(3)Catergory-3
Category-1/2中的个体随意地进行移动,但实证数据中发现显著的周期性访问模式。为了解释这些观测,个体移动模型(IMM)将人类移动行为看作两个阶段:return/exporation来解释长时记忆效应。
提出偏好返回机制,即返回先前访问过得位置

与历史访问频率成正比,这样的长时记忆返回过程大大减缓了人类的扩散过程。
IMM预测典型移动距离
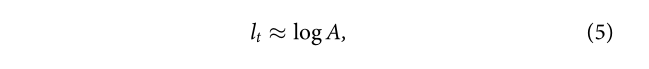
其中A是访问位置的总体数目。对数增长是人类移动的关键特征,描述了异常的极慢扩散和活动范围的影响。
d-EPR模型对IMM模型进行了推广,个体探索新位置的概率与其人口密度呈正比。
即使d-EPR和IMM模型都成功捕捉了日常个体的移动,但个体独立的移动并且不与其他个体相互作用,是静态的且不随时间演变。这个模型不能捕捉个体之间的动态交互,也不能再现城市增长模式。
(4)Category-4
既包含社会关系也包含长时记忆的模型很大程度上是没被探索的。最近提出的GeoSim模型将社会网络(每个个体更倾向于探索他们朋友访问的位置)与有记忆的IMM模型结合,然而社会网络需要根据实证数据提前确定,不随时间演化,也无法长时间追踪城市增长。
The collective mobility model
为了结合长时记忆与动态交互关系,本文提出群体移动模型(CMM),提供了将人类移动与城市增长联系的最小原则。
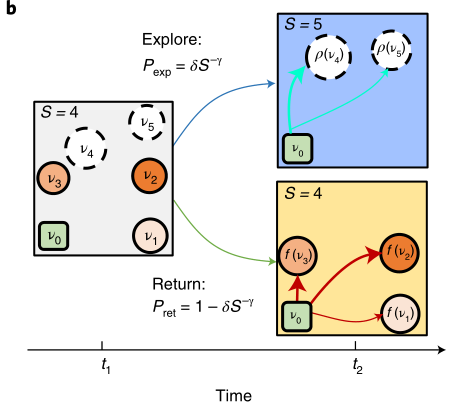
该图为CMM模型的图示。在时间
在该模型中,个体的移动依照IMM模型中return-exploration过程,个体决定返回到先前访问过的地点的概率为
个体同样具有互补的探索概率
受具有强空间相关性的相关渗流模型的影响,本文对具有强耦合
CMM模型可以在任意时间尺度下以自组织的方式模拟城市增长并且不依赖任何外部参数。
Experimental settings
本文使用三个包含人口的城市区域的公开数据集(US/GB(英国)/柏林)
为了对比,本文使用category1-4的模型(莱维飞行,引力模型,IMM,CMM)进行人类移动的模拟。
该模拟在一个l×l的二维仿真空间中进行的,模拟的居民初始位于城市中心,即仿真空间的中心点。随后在每个时间步迭代他们的下一个位置直到模拟收敛。
Urban morphology
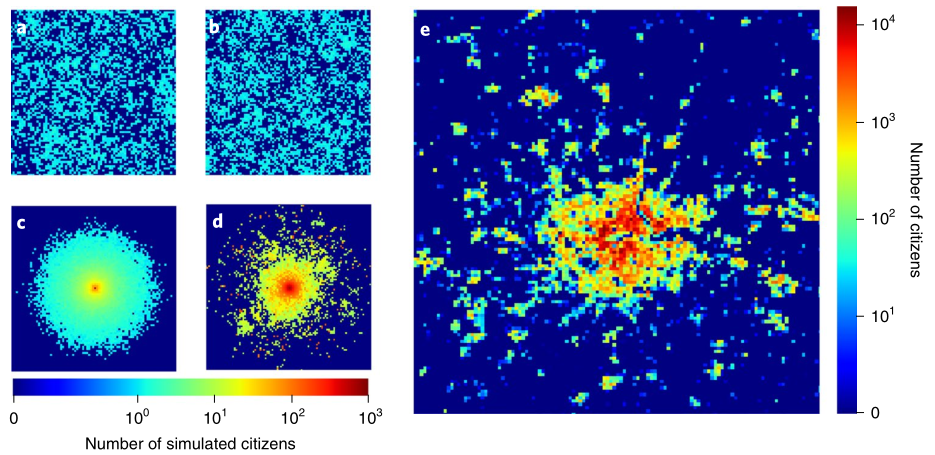
该图画出人口分布图来比较模拟城市系统和实证观测的城市形态。图a-d分别由莱维飞行、引力模型、IMM、CMM生成,图e为伦敦城市的实证数据。
实证数据中表现出显著的特征:紧凑的城市中心和碎形的周边。
莱维飞行和引力模型模拟的城市人口分布遵循分数阶扩散过程(the fractional diffusion process),都意味着随着时间推移,个体会逐渐远离他们的初始位置。模拟结果证实这两种模型不能再现紧凑而稳定的城市中心,收敛时人口在城市空间中均匀分布。
IMM预测城市系统在边缘同质增长,模拟结果显示城市区域的周边是标准的圆形,距离城市中心相同的径向距离有相同的人口密度。IMM模型不能再现城市区域的碎形形态。
CMM成功再现了城市系统中紧凑的城市中心,人口密度大幅度高于城市周边。此外,城市周边具有明显的碎形几何特征,并在其周围形成了大量的子群,这些观测与实证数据一致。
Urban growth patterns
本文通过三个基本的实证定律检验模型再现城市增长模式的能力:
(1)城市规模分布: 城市数目N(A)随他们的面积减小符合标度律
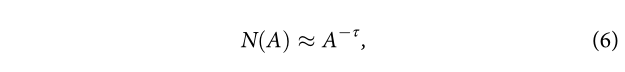
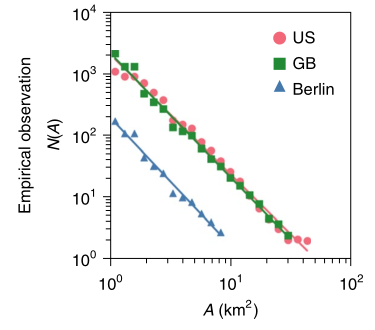
指数在2.0左右。
该图为实证数据中城市大小的分布。在三个数据集中的估计指数分别为1.94,2.01,2.08,这些发现与位置渗透理论(site percolation theory)的理论预测相一致。。
渗透理论是描述这一观测结果的普遍框架,其产生某个位置被占用为城市区域的概率。它预测了(6)式的标度律指数在2.0-2.5左右,其中指数为2对应不同位置之间的强相关,指数为2.5对应平均场理论。
莱维飞行将移动描述为个体的扩散过程,城市系统达到稳态时,城市人口在空间中均匀分布。与莱维飞行相同,当t趋近于正无穷时,人口也会均匀分布。因此,莱维飞行和引力模型预计将在不相关渗流(uncorrelated percolation)中生成指数为2.5左右的标度律。
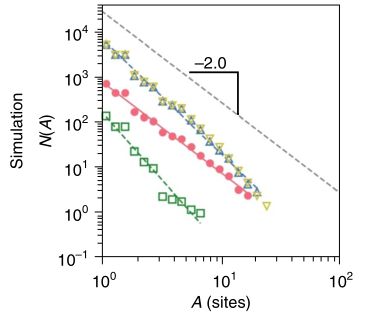

该图展示了莱维飞行和引力模型再现幂律城市大小分布,指数为2.55和2.58,与渗透理论一致。
模拟的IMM符合指数为2.98的标度律。这个较大指数意味着人们只局限于他们的活动范围。
相反,CMM展现出强相关性,其再现了指数为2.02的标度律,与理论预测和实际数据一致。本文发现CMM是唯一一个在95%置信区间内包含实证观察到的普遍指数为2.0的模型。
(2)人口和城市规模的超线性相关:
大城市往往有较高的城市人口密度,定义为
(N(A)代表区域A中城市的数量)
研究人员认为因为在大城市的空间竞争更激烈,故有更多的高层建筑来应对更密集的人口。
最近的研究表明,城市区域集中人口收支之间的平衡可以解释观测到的超线性增长。这个社会经济假说包含两条假设:
从强烈的社会互动中获得的平均收入与人口密度
成正比 (与(3)式中社会互动一致)
平均生活支出与探索城市的典型移动距离
成正比 (与(4)式中长时记忆效应一致)
收支平衡时有
代入等式(5)(典型移动距离
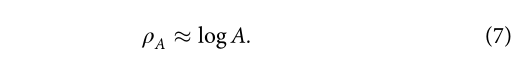
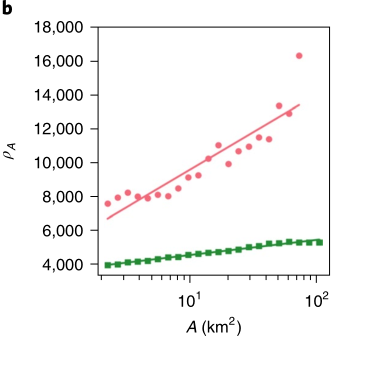
该图绘制了在US和GB不同城市中
值得注意的是,之前的研究显示,大多数城市遵循小指数
式(7)中指出的对数关系为人口增长模式的起源提供了另一种解释,它源于人类移动行为。
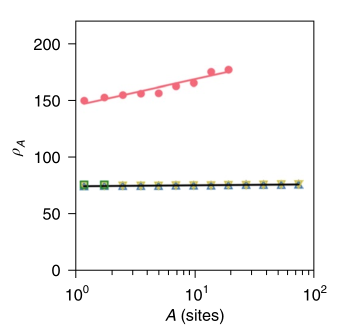
该图为四个模型模拟的城市人口密度与城市规模之间的关系。
本文提出的CMM模型再现了对数律,其他三个模型用系数为0的直线进行拟合,说明它们预测人口密度独立于城市规模。
(3)指数的城市占有概况(occupation profile)
城市占有概况
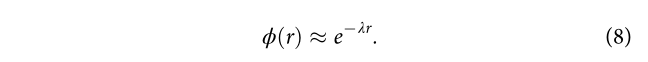
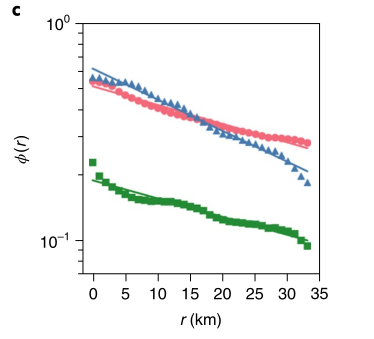
该图为在三个实证数据集中对该模式的检验,其中
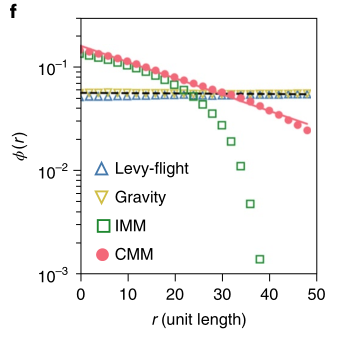
该图为四种模型模拟的城市占有概况。莱维飞行与引力模型不能再现城市中心,预测的
此外,下降率
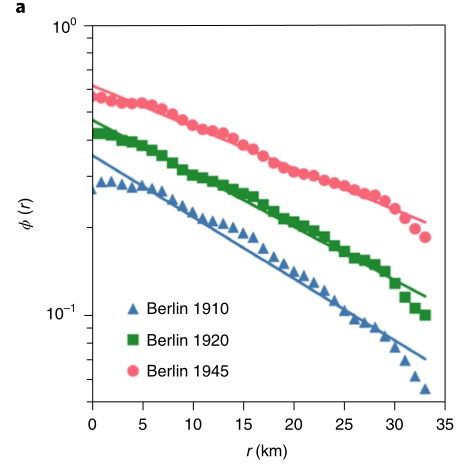
该图展示了实证数据柏林的城市占有概况的时间演化。从图中可以看出,随年份增加,降低速率逐渐变缓。
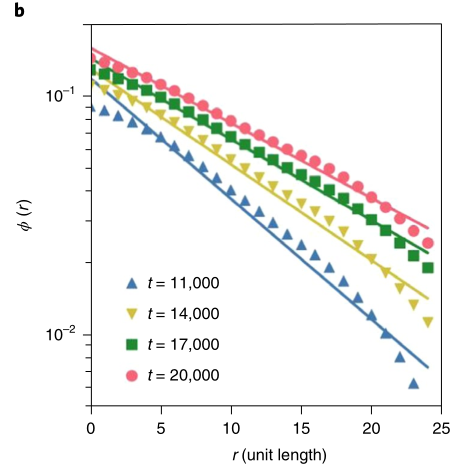
CMM模型的模拟结果再现了城市发展中占用概况的时间演化。
Impact of simulation parameters
有三个重要的参数可能影响城市系统的模拟
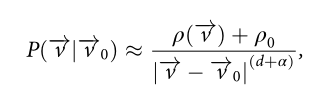
(3)式中的
描述主要移动距离成本,控制每个位移的距离分布
(3)式中的
主要控制社会互动的重要性,它决定个体探索更多人口密集地区的概率,
时再现强互动性的城市系统。 平均人口密度 定义为居民人数与位置数的比率,即
它代表个体在每个单位空间中社会互动的数量。

该图为CMM模型不同参数数值再现城市形态的比较。
标准参数设置为
在图a-f中对模拟中单个参数值进行修改,其中
(a)
(c)
(e)
(1)
图ab表明
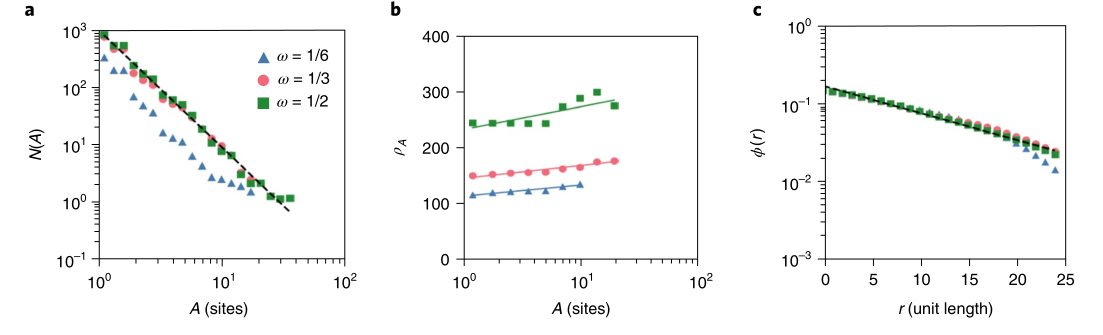
该图为设置不同
城市规模分布,人口增长模式和城市占有概况在不同
这个结果表明城市的增长模式在不同
(2)
当
当
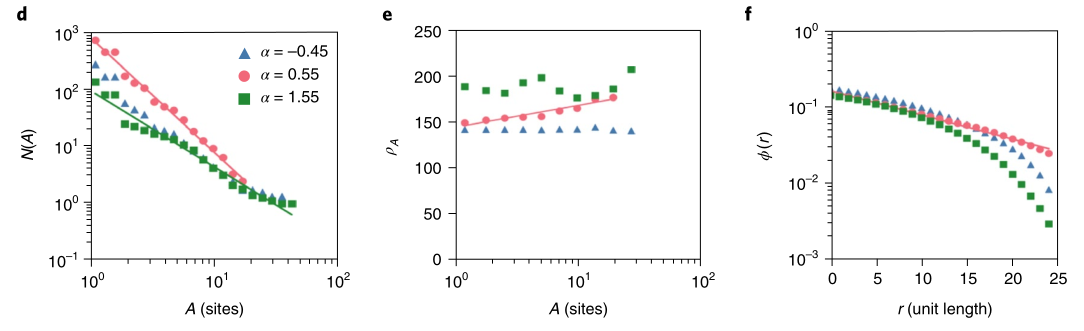
该图为设置不同
当
(3)
该参数很大程度上影响了城市区域的形态。
图e展示出显著的碎形形态(
当将
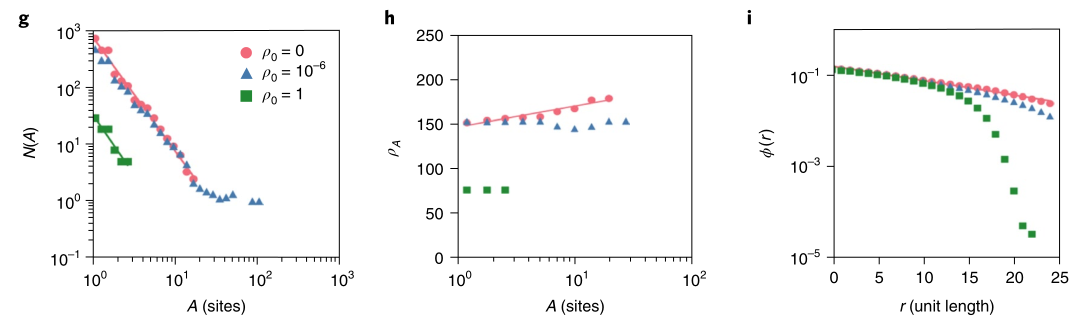
g图表示城市规模分布的指数随
h,i表示当
这些结果说明参数
Disscusion
本文试图建立城市增长与人类移动之间的关系。
值得注意的是,尽管大多数人类移动模型都基于以日常移动为主的活动性移动行为,但城市增长与居住移动(即居住迁移)的关系更为密切。尽管这两种移动是在不同时间尺度下的人类移动,但是它们在表现模式上有相同特征。CMM模型通过不同的参数设置为活动性移动和居住性移动提供框架(例:居住性移动有更小的转移率)。
Supplementary
留坑了……
标度律
研究模型内的各个物理量是如何随着规模的变化而变化的
平均场
mean-field
渗透理论
percolation theory
强相关性与不相关(uncorrelated percolation) 平均场
总结及理解
理解
1.d-EPR模型虽然包含个体探索正比人口密度的机制,但仅限于个体层面,是静态的且不随时间演化,故与社会关系无关。
涉及引力模型中提到的平均场与背景场概念。
2.
3.IMM模型在标度定律(1)中指数较大说明假设在同等面积下,所具有的城市数量越少,这与其模型机制只包括个体,不具有社会关系有关,故个体更局限于自己的活动范围。
4.城市占有概况的指数律说明大部分人集中在城市中心,周边聚集情况大幅度递减,而式(1)中提出人类移动符合胖尾分布,即人类有可能到达远离初始位置的区域,这两点是相矛盾的。故在模拟实验中莱维飞行和引力模型不能再现该指数律。
总结
本文从社会和记忆两个角度对之前提出的人类移动模型进行分类,并提出同时具有社会互动和长时记忆机制的群体移动模型(CMM)。随后从城市形态(人口分布)和增长规律模式两个方面,对原有模型/提出模型/实证数据进行对比,并设置不同参数来观察对CMM模型的影响。
组会结束之后对该文有了更深层次的理解。该模型是对基于个体移动模型的改进(原EPR模型),主要的改进是探索机制中使用引力模型相关距离和人口的转移概率,特点是进行实时的动态人口计算。
其中组会提出的问题:城市周边分形出现的原因?
与动态的人口计算有关。假设在模拟过程中,下一个位置探索选择的概率与此时各位置所在人口有关。如果该位置此时没有人口,则不会有个体选择该位置。所以可以说选择的概率二分了,要不有要不没有,所以城市周边会产生碎形(即小子群)。若是静态输入人口密度,采取累加的方法,则每个位置至少有一定探索概率,不会出现完全没有的情况。
该模型同时存在缺点:只考虑时步,没考虑stay
- 本文标题:Emergence of urban growth patterns from human mobility behavior
- 本文作者:y4ny4n
- 创建时间:2021-09-05 12:55:05
- 本文链接:https://y4ny4n.cn/2021/09/05/101/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!