Limits of Predictability in Human Mobility

提出一个问题:人类行为在多大程度上是可预测的?

通过测量每个个体的轨迹熵，作者发现用户的移动有93%的潜在可预测性

尽管个体在移动模式上有显著差异，但作者发现可预测性显著缺乏变化，很大程度上与用户定期移动的距离无关。

本文认为，在我们的直觉和当前的建模之间存在着根本性的鸿沟:

尽管我们很少认为我们的任何行为是随机的，但从一个不知道我们的动机和计划的外部观察者的角度来看，我们的活动模式很容易显得随机和不可预测。

但是，现在关于人类活动的模型基本上都是随机的。

在何种程度上，个体的行为是可预测的?

本文旨在通过人类移动探索可预测性的界限，量化规律(可预测)和随机(不可预测)之间的相互影响。

Data

观察期为3个月

从~1kw筛选出5w个体(访问超过两个地点，通话频率)

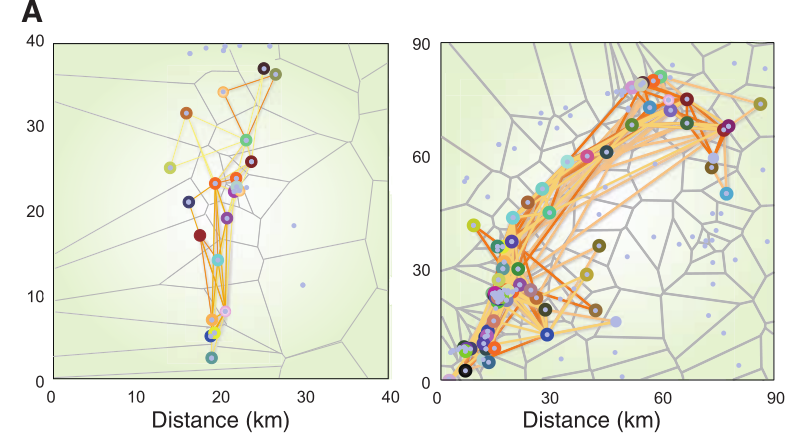
该图展示了两个移动模式不同用户的轨迹:

第一个用户在30km内移动了跨越22个信号塔的附近区域

第二个用户在90km内移动了跨越76个信号塔的附近区域

灰色线条代表对应塔的信号接收范围

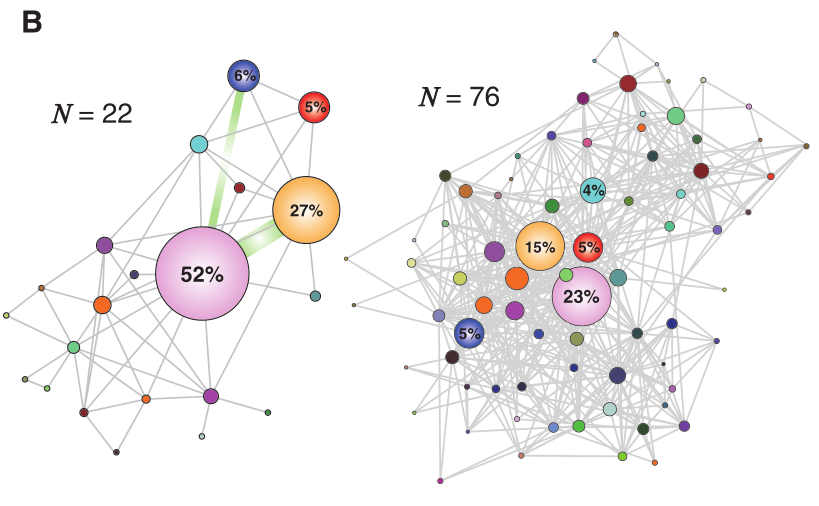
该图展现了上面两个用户的移动网络。

节点大小代表在该塔附近的通话频率(用户在该塔附近花费时间百分比)，线的宽度与在两塔之间的移动频率成正比。

每个移动网络都有一个相关的动态模式，捕获用户访问塔的时间序列

该图表示第一个用户在一周内访问位置的时间序列。每一条竖线代表一次通话，颜色代表此次通话所在塔。

Results

Entropy(pt1.)

熵可能是描述时间序列的可预测性的最基本的量

本文定义了三个熵测量了每个用户的移动模式:

随机熵: 是user i访问过的不同位置数

如果访问每个位置的概率相等，得到用户所在位置的可预测性程度
时间不相关熵:

是user i曾经访问位置j的概率，表现了访问模式的不同性
实际熵:

实际熵不仅取决于访问频率，还包括访问节点的顺序和在每个位置花费的时间，故能捕捉到人移动模式的完整时空顺序。

表示在每连续的一小时间隔用户i所在的位置的序列

是在轨迹中找到特定时间顺序子序列的概率

为了计算实际熵，我们需要用户连续的(例如每小时)位置记录。但用户倾向于在短时间内拨打大部分电话，长时间内不进行通话，在此期间无法获取用户位置。由图C可以观察到间断性与突然爆发。

参数q描述收集数据的不完整性，表示用户位置未知所占比。

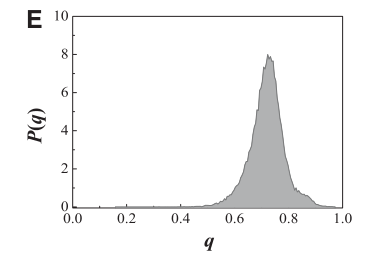
该图为q的数据集中的分布。峰值在q=0.7附近，说明对一个用户，我们有70%的时间间隔没有位置更新，掩盖了用户的实际熵。

因此本文研究了不完整性的熵S(q),允许推测q=0时的熵。(?)

作者通过100个每小时都被记录位置的用户测试该方法的准确性，发现q<0.8时表现良好，即数据集的92%。故移除5000个q最高的用户，使剩余用户满足q<0.8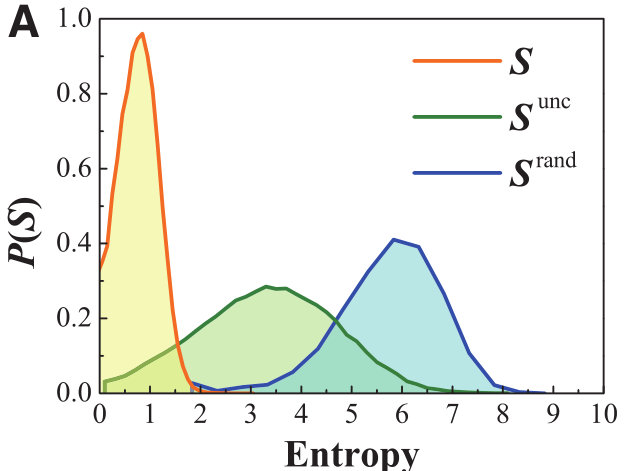

该图为三个熵在数据集上的分布。=6达到峰值，说明：用户位置的每一次更新代表每小时6位的新位置，即用户随机选择他访问新位置的范围是个。

但是真实熵在S=0.8达到峰值，说明真实情况不是64个位置的范围，而是 ,少于两个位置。

pt2.

本文随后表示数据集中用户的回转半径符合胖尾分布，虽然大多数个体活动限制在1-10km，但也有一些用户经常移动覆盖数百千米。

这些差异表明，用户移动的可预测性也应该符合胖尾分布。即移动少的个体(熵小)应该更容易预测，移动多(回转半径大，熵大)更不容易预测。

本文使用参数来表示适当的预测算法可以正确预测用户未来的位置的可能性。

如果用户的熵为S,访问了N个位置，则他的 ,通过以下给出

(二项分布的信息熵)

如果一个用户的 ,说明至少80%的时间下,个体选择地点的方式是随机的，我们仅可以在20%的时间内与预测他的行踪。代表个体可预测性的基本极限。

作者对的分布进行了统计，发现其并没有符合前边所说的胖尾分布，且在附近达到了峰值。

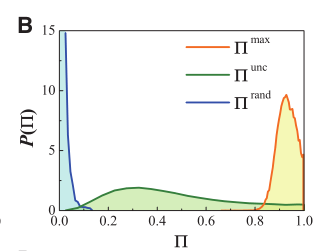
这说明尽管这些个体的移动轨迹具有明显的随机性，但用户移动模式的记录隐藏着一种高度潜在可预测性。

作者还通过时间不相关熵和随机熵计算了对应的可预测性。

其中，的分布表现出覆盖很宽，峰值在0.3左右，这说明如果我们只依赖于不同的空间分布，那么整个人口的预测能力是微不足道的，而且人与人之间差异很大。

在0达到峰值，这说明该参数对预测没有作用。可预测性被加密隐藏在访问模式的时间序列中了。

pt3.

如何使捕获的回转半径的广泛可变性与整个用户群体中观测到的高度可预测性一致?

本文绘制了与回转半径的相关性

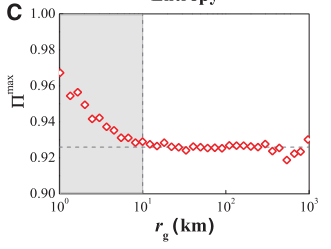
当回转半径≥10km时，可预测性在很大程度上与回转半径无关，在左右趋于饱和。这解释了前面提出的假设失败:个体回转半径≥100km,定期覆盖数百千米和回转半径在10km以内的用户同样可以预测。

pt4.

为了了解可预测性在多大程度上取决于移动模式中最常去的位置，作者计算了在给定时刻，用户处于最常访问n个位置之一的概率。因此，代表的上界。

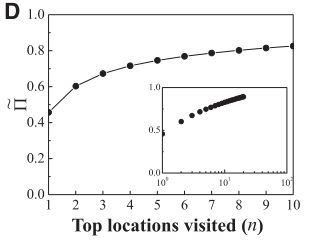
当n=1,我们可以预测用户的位置在最有可能的位置(“家”)

当n=2,我们可以预测用户的位置在他最常访问的两个位置之一，家或办公地。仅有60%的可预测性。

随n近似对数增长，当添加更多位置时，可预测性随之增长。

pt5.

为了理解观察到的潜在可预测性的来源，将每周划分为168小时间隔，在每小时内确定每个用户在该时间内访问最多的位置。

计算每个用户的规律性R，定义为在用户访问最多位置找到用户的概率。R表示可预测性的下限，因为其忽略了个体移动的时间相关性。

在整个用户群中，R≈0.7 这说明70%的时间，访问次数最多的位置与用户的实际位置一致。这种模式与时间相关:大多数人晚上待在家里，此时R的峰值为0.9;但在中午到下午1点和下午六七点之间，R有明显的极小值(上下班高峰)。

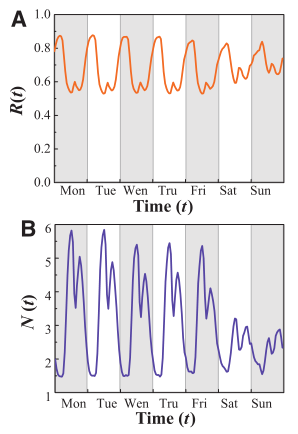
图A表示在对应的时间间隔内，用户在他最常访问位置的比例(规律性R)。

图B表示在对应的时间间隔内，用户访问位置数目。

高的规律性对应着小的数目，当R达到顶峰，N下降。

如果用户在N个位置之间随机移动，，比观测到R≈0.7小一个数量级。

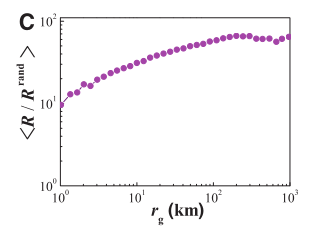
该图表示与回转半径相比，表现出回转半径大的用户有更高的相关规律性()。

也就是说，相反，移动次数多(回转半径大)的用户比在家较多的用户具有更高的相关规律性。

作者没有观察到在性别或年龄上有明显的差异，且家庭、语言群体、人口密度、城市与农村环境等因素对可预测性的影响只有微弱差异。与工作日相比，没有发现用户周末出行规律性有显著变化。这些都说明该规律性是人类活动潜在固有的。

pt6.

回转半径大的个体移动并非没有什么可预测性，最大的可预测性变化非常小。达到93%的峰值，且在数据集中没有任何用户可预测性低于80%。

虽然明确预测用户的位置超出了我们能力范围，但适当的数据挖掘算法可以将我们研究中确定的可预测性转化为实际的移动预测。