Modeling the scaling properties of human mobility

个人移动轨迹的jump size()和waiting time()符合胖尾分布，这说明连续时间随机游走模型(CTRW)与人类移动的相关性。

我们需要能描述移动轨迹统计特征的定量模型。本文使用人类移动的经验数据(empirical data)来说明CTRW模型的预测与实证结果存在系统性冲突。

本文介绍控制人类移动的两个准则，建立一个个体移动的统计微观模型。该模型解释了经验观察到的标度定律(scaling laws)，同时也允许我们分析预测大多数相关的标度指数。

Introduction

即使众多可用数据集在范围和分辨率上有显著不同，但在人类移动的一些定量特征上表现出一致。

例如，美钞的追踪和移动电话数据都表明描述人类移动轨迹的聚合jump-size()和waiting-time()符合胖尾分布，表示连续观察之间个体移动覆盖的距离，表示个体在同一位置花费的时间。这些发现说明个体移动轨迹可以被莱维飞行(Lévy flights)或CTRW很好地描述。

本文的目的是说明通过一系列的直接测量，个体移动轨迹遵循几个高度可复制的标度定律。然而这些定律中的许多要么不能被CTRW模型解释，要么直接与CTRW预测相矛盾，这说明缺乏一个能捕捉人类移动基础特征的模型框架。

为了解释观测到标度定律的来源，本文介绍了控制人类移动的两个准则，作为个体移动统计微观模型的起始点。本文提出的模型可以解释实证观测到的标度定律并允许我们分析预测相关的标度指数。

Scaling anomalies

本文使用两个数据集描述个体移动模式的特征。

D1记录了一年时间内三百万匿名移动手机用户的移动轨迹(CDR)。

D2记录了1000名注册基于位置服务的用户的位置，他们的位置在两周内每小时进行记录。

首先计算每小时位移，发现其符合~并在~100km处截断。

使用D2测量,发现其符合~并在处截断。

以上观测到的分布结果遵循CTRW模型。

作者提出以下三个实证观测结果，表明人类移动轨迹遵循可复制的标度定律，但也说明了CTRW模型在捕捉观测到的标度性质上的缺点。

(A)访问的不同位置数

一个随机移动物体访问不同位置的数目遵循~

在莱维飞行中，在CTRW中

本实验数据中观测到的，小于CTRW预测的

说明访问不同位置数在大时间尺度上的减缓，用户访问之前没访问过地点的趋势减少。

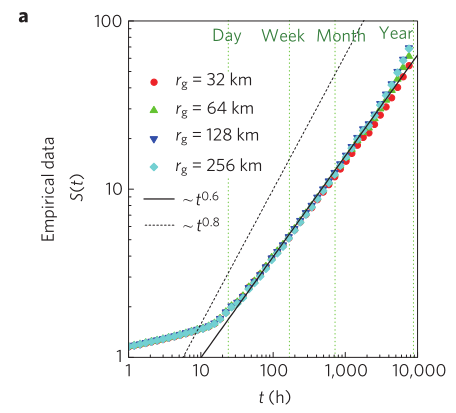
该图表现出不同的回转半径对应的访问位置数。

(B)访问频率

在莱维飞行和CTRW模型中一个用户访问给定位置的概率是处处渐进(t )一致的(f~const.)。

相反，人类访问模式相当不均匀，k-th最常访问位置的访问频率f遵循Zipf’s law

这说明访问频率的分布遵循~

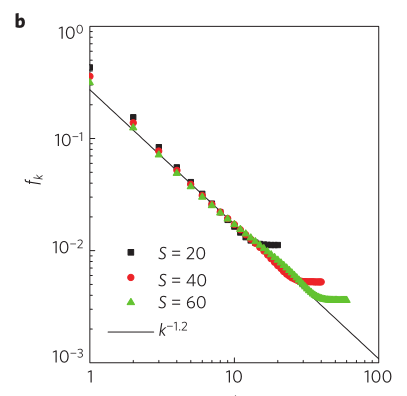
该图反映出不同S值下用户访问k-th最常访问位置的访问频率，实证数据很好地被~拟合。

(C)极慢扩散

CTRW模型预测均方距离(MSD)渐进符合 ()

和P()与P()都有截断相同，MSD在时收敛为布朗运动

然而这种收敛在我们的观测时间范围内太慢，不具有相关性。

CTRW模型预测我们观测个体的移动轨迹时间越长，他就会越偏离初始位置。

然而，人类每天都有回家的倾向，这说明简单扩散过程在二维空间中不循环，不能提供对人的移动进行描述。

本文的测量观测到了极慢扩散过程，MSD遵循一个比对数更慢的增长(对数增长:对数增长初期进步速度非常快，后面会越来越慢，最后几乎处于一个平台期)。MSD的极慢增长在扩散中是罕见的。

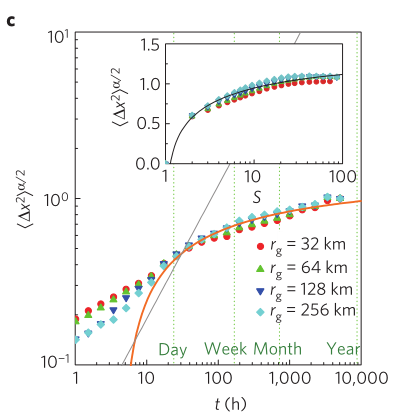
该图说明用户组的MSD()在不同的回转半径下的时间演化。使用t=1year的值对MSD值进行归一化。

橙色曲线表示渐近行为的分析预测，灰色曲线代表CTRW模型的分析预测。

插图:归一化MSD值在不同回转半径下比访问位置数S。

A-C的发现说明人类个体移动却是遵循可复制的标度定律，它的起源还有待发现。它们仍然说明莱维飞行和CTRW等空模型预测的系统性差异。本文的主要目标是提出一个不仅能解释异常A-C起源的模型，而且是描绘人类个体移动的自洽统计模型。

Generic mechanisms and individual mobility model

建立模型时，作者遵循一系列模型的结果认为jump-size和waiting-time符合胖尾分布。

但只符合和的分布不足以解释标度定律A-C。

作者提出造成这种差异的主要原因是两个生成机制，exploration(探索)和preferential return(偏好返回)。这两个机制都是人类移动特有的，且在传统随机游走模型(莱维飞行/CTRW)中缺失的。

(1)Exploration

随机游走模型假定扩散的下一步独立于之前访问的地点。相反，标度定律A说明探索额外的位置的趋势随时间逐渐减小。

我们观察一个人的移动轨迹越久，就越难发现在他家/工作地附近还没访问过的位置。

(2)Preferential return

与随机游走模型的访问概率在空间中是随机和统一的相反，人类有明显的倾向返回他们之前频繁访问的位置，例如家或工作地。

本文提出包含以上两个机制的模型，能充分解释异常A-C。

该模型用来描述个体的移动轨迹。假设t=0时，个体在一些首选位置。经过waiting-time()后在分布P()中选择改变他的下一个位置。

我们假设个体有两个选择:

(1)Exploration:

个体移动到一个新位置(不同于他之前去过的S个位置)的概率为

他移动覆盖的距离在分布P()中选择，方向随机选择，移动位置数S+=1。

(2)Preferiential return:

个体返回之前访问过的S个位置的概率为

访问位置i的概率与该个体之前访问过该位置的次数成正比。

在网络或社会科学中，这一假设被称为 preferential attachment/ cumulative
advantage。

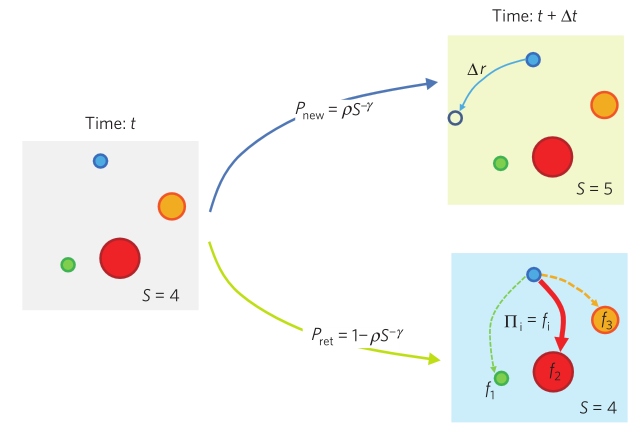
该图描述了本文提出的个体移动模型。从时间t开始，该用户之前访问过4个不同的位置(访问频率f和每个位置圆的大小成正比)。在时间t+，该用户可以选择访问离他现在位置的新位置，也可以返回到他之前访问过的位置，该位置由访问频率f决定。

Model predictions

本文提到该模型适用于捕捉长期尺度模式，不能再现人类移动短期内的时间顺序和潜在相关性。我们选择关注渐近性质(asymptotic properties)不仅仅是由理论驱动的(旨在重现普遍模式而不是短暂模式)，也是出于实际考虑:许多人类移动驱动过程，从疾病传播到城市规划，都是由人类移动的渐近特征驱动。

为了实现短期时间更好的还原度，我们加入了人类移动特征的周期调整(24h和7d的周期;个体在晚上很少移动，在早上和傍晚更多移动)，也加入了空间移动的潜在相关性(B地在A和C之间,访问顺序A→B→C或C→B→A)。这些相关性进一步限制了人类的轨迹，在一定程度上是个人移动模式具有高度可预测性的原因。

提出动态抑制(dynamical quenching)和重复行为是人类轨迹独有的，本文提出的模型代表了对CTRW/Lévy-flight模型的改进，因为它捕捉人类流动性的特性。

补充

1.Zipf’s law

https://blog.csdn.net/historyasamirror/article/details/3125223

在自然语言的语料库里，一个单词出现的频率与它在频率表里的排名成反比。

2.MSD

http://blog.sciencenet.cn/home.php?mod=space&uid=3388193&do=blog&id=1232344

即均方位移(the mean square displacement )

在统计力学中，均方位移（MSD，均方位移或均方波动）是粒子随时间移动后的位置相对于参考位置的偏差的量度。它是随机运动中空间范围的最常见度量，可以被认为是对随机行者“探索”的系统部分进行度量。

MSD定义为t时刻的系综平均(集平均，某一时间点随机变量的期望)：

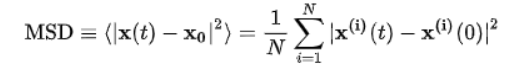
3.渐近分析