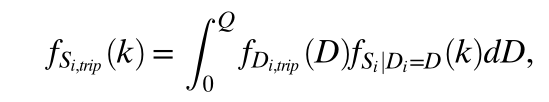The TimeGeo modeling framework for urban motility without travel surveys

y4ny4n
  2021-12-25 16:01:55 2021-12-25 16:01 创建   2024-02-29 09:51:43 2024-02-29 09:51 更新      4.4k 字  15 分钟  

许多精细尺度的城市流动模型都需要繁琐昂贵的出行调查来校准，且这种出行调查成本高采样率低。

本模型旨在对通讯技术提供的大量低成本地理标记数据(无法告诉我们用户的详细活动选择)进行根本性的范式转换，以模拟城市流动。

本文提出的TimeGeo模型可以在10min时间间隔和百米的分辨率下高效产生城市流动模式，从通信活动中可用的稀疏和不完整的数据中生成完整的城市流动概况。

Data

手机通信数据具有采样偏差，不能为每个人提供完整的空间和时间旅程。需要一种的范式转换适应这种稀疏数据来模拟城市中个人的日常轨迹。

从移动通话数据中提取活动

  • CDR data
  • 1.92 million

  • 6 wk in 2010

  • Greater Boston area

做对照实验，使用一个研究生捐献的自收集长达14mon的移动手机轨迹。( same region,in 2013 and 2014)

定义停留(stay):个体在某一地点进行某一活动(stay提取方法参考文献23)

对于每个用户，根据开始时间和访问每个stay地点的频率，推断stay地点类型为家(H)、工作(W)或其他(O)。

在数据集中过滤活跃用户:提取数据集中原始用户75%的家坐标，并过滤总stay超过50次并至少在家stay10次的用户。这些活跃用户用来提取TimeGeo模型的参数。

作者将这些用户分为通勤者(有往返工作地的出行)和非通勤者(没有往返工作地的出行)两类。

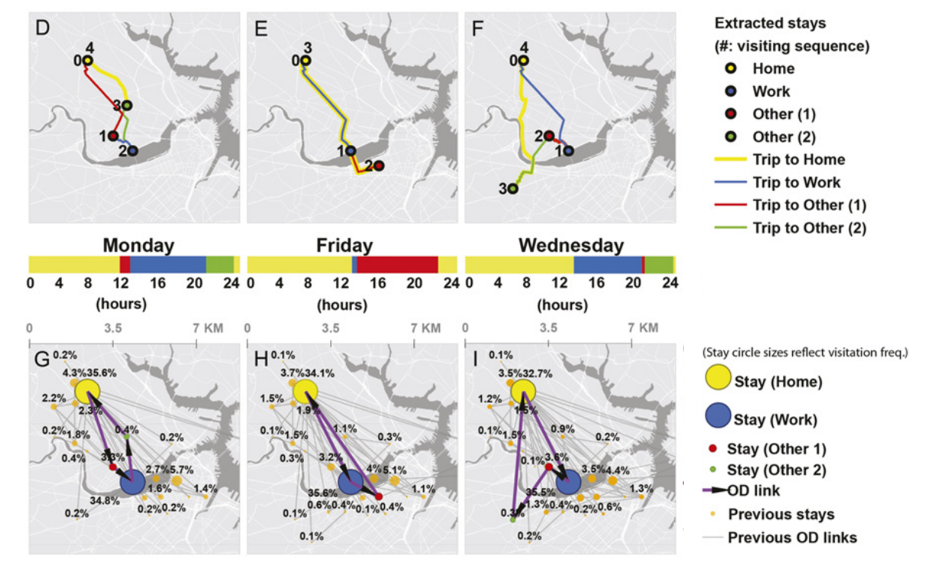
image-20211105175523819

该图展示了三天中学生自我收集的移动轨迹中stay的地点和在连续的stay之间发生的移动(即定义为每天的行程)。不同活动类型地点及其之间的连线用颜色区分。

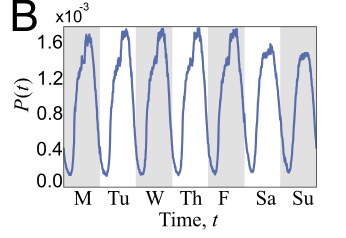
下图是所有stay地点的访问频率，两图之间的时间条显示了每次stay的开始时间和持续时间。

Generating Mechanism

该模型整合了人类移动的时间空间选择机制。

本文假设个体:

  • 工作活动有固定的位置，开始时间和持续时间

  • 家活动有固定的位置，但开始时间和持续时间是灵活的

  • 其他活动的位置，开始时间 ，持续时间都是灵活的

本文提出的框架旨在模拟灵活的空间和时间流动性选择，固定的活动(即工作)的时间被假定为预先确定的。

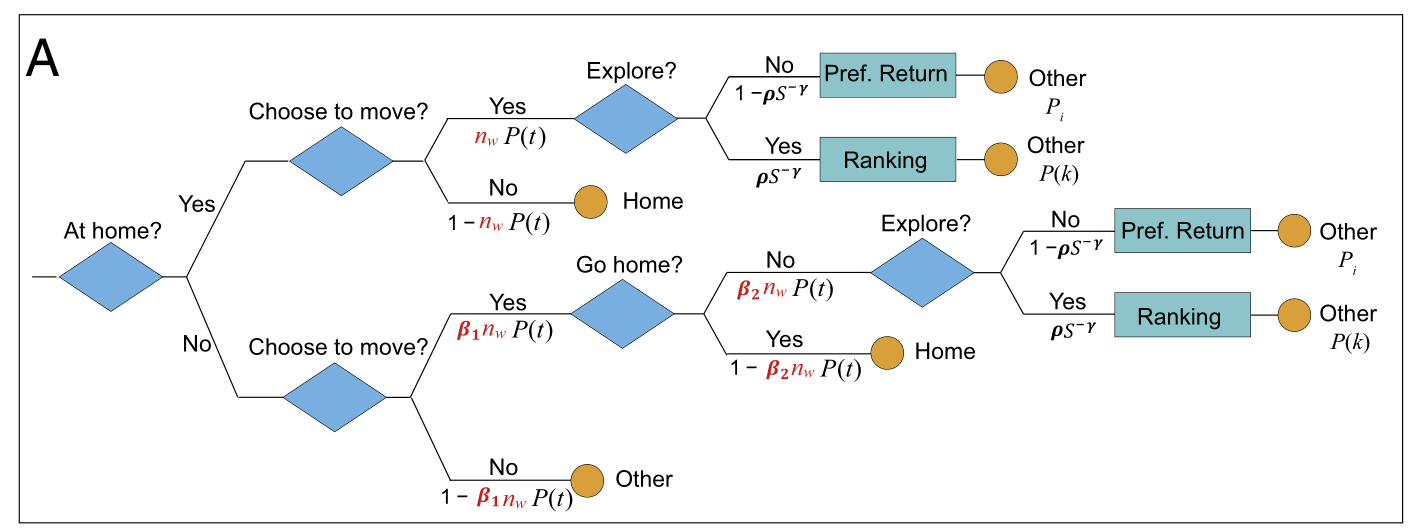
image-20211111214439699

TimeGeo模型的流程图

Temporal Choices

文章使用带有三个参数的time-inhomogeneous(?非齐次)马尔科夫链模型来捕捉个体出行的倾向和在连续序列中进行短时间活动的可能性。

参数:the weekly home-based tour
number(), the dwell rate(), and the burst rate().

考虑两个状态:home和other。Home被认为是一个活跃度较低的状态，因为home状态的平均停留时间显著长于other状态。

1.个体在home状态出行可能性

当个体在家时，他的出行倾向被定义为，代表他在一周内t时间间隔从家出发进行移动的可能性。其中:

  • 统计了个体从家出发去其他位置移动的总数。

  • P(t)是在平均一周内全部人口的出行倾向。

    对通勤者和非通勤者来说，P(t)不同:

    • 非通勤者:在一周内的时间间隔t所有人口的出行数占所有出行的比例。(即)，捕捉了在一周内不同时间出行的预期变化。

      image-20211111203522748

    • 通勤者:P(t)不包括往返工作地的出行(工作被看作是固定的活动)

两者的乘积，定义了个体在家时在特定时间间隔t出行的概率。

2.个体在other状态出行可能性

为了刻画个体在other状态出行的倾向，作者介绍了dwell rate，衡量了个体在相较于home状态的other状态的活跃(倾向出行)程度。

当一个个体在other状态的出行概率被定义为。通过捕捉个体从other状态移动的倾向，控制了活动的停留时间。其乘积越大，个体更倾向移动，所以他停留在其他位置的时间越短。

3.在other状态选择移动后是否回家(选择连续进行out-of-home活动的可能性)

如果个体已经out-of-home，并在时间t选择移动，作者通过burst rate 来刻画他回家或者去其他额外位置 的选择。

定义个体从一个other位置O1到另一个额外other位置O2移动的可能性为

假定个体已经决定移动，他访问额外的other位置的概率正比于。回家或去额外的other位置两个选择的比率为:

对于给定，当P(t)高时(代表在当前时间段人们倾向出行),人们更有可能访问额外的other位置;当P(t)低时,人们更有可能回家。

对于给定P(t),值越高，个体有更高的概率保持访问other位置，故他每天访问地点数N大。

Spatial Choices

a rank-based exploration and preferential
return (r-EPR) mechanism(在原始EPR模型中结合基于空间距离的排名)

原始EPR模型的限制为缺少探索中选择新位置的机制。原始EPR模型随机在实证jump-size()分布中抽取距离。为了描绘更能反映城市结构的探索机制，在本文中结合对探索新的位置基于排名的选择机制，即r-EPR模型。

选择机制:基于距移动始发地的距离，给每个可选目的地排名。在所有潜在的新目的地中，离现在位置最近的k=1…

将第k个位置作为目的地的概率被量化为

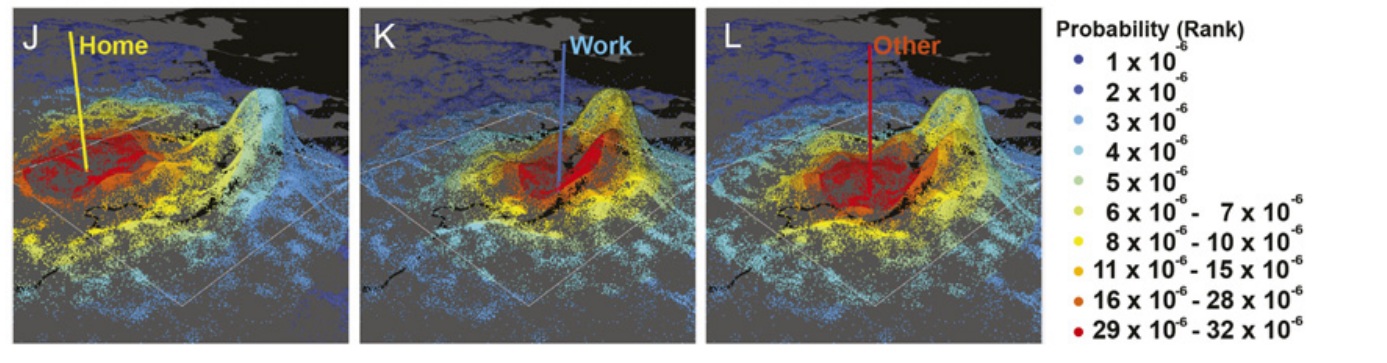
image-20211112144732374

该图为对r-EPR模型的图示。可能的目的地使用颜色对不同选择概率进行区分。 地点距始发地越近，它被选择的概率越高。每个点代表从CDR数据中提取的进行other活动的位置。点的高度代表在附近区域可选目的地的密度。

Role of Land Use on Travel Distance

为了解释和量化土地利用(land use)对出行的影响，本文提出a hierarchical multiplicative cascade(层次乘法级联模型)进行分析。

TimeGeo将位置的空间分布(在CDR数据中观测到的)作为输入。

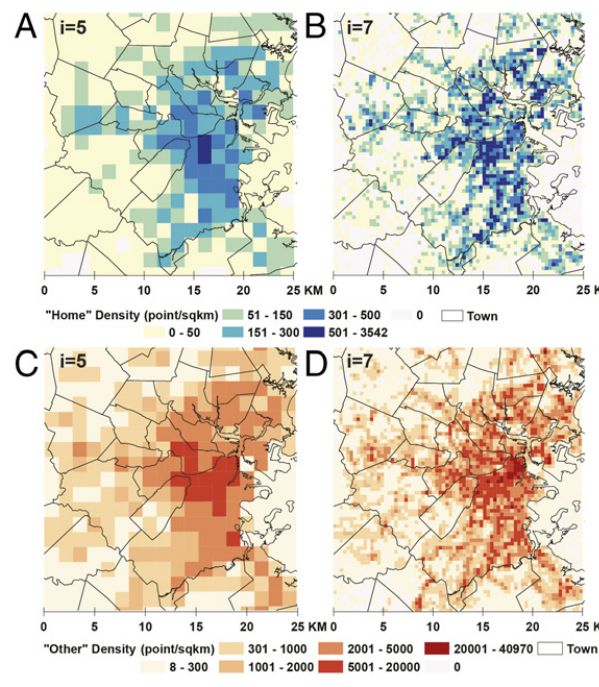
image-20211112151048619

该图展示了不同类型的位置(home/other)在两个尺度下的分布。AB图是home位置在不同分辨率下的分布，CD图释other位置在不同分辨率下的分布。

在较大网格尺度下，home和other位置在空间上是混合的，表现出高度的空间相关。在较小网格尺度下，home和other类型的土地利用分离变得清晰。

层次乘法级联将感兴趣的区域划分为不同粒度的网格，量化不同尺度下各类土地利用的空间相关性。

当前框架结合了影响探索机制空间选择的两个特征:(i)活动位置的空间分布 (ii)基于排名的位置选择。

为了量化家到Other位置(H-O)的出行距离，作者提出将家位置作为需求方D，other位置作为提供方S。

需要分析的整个区域为，作者渐进地使用边长将其分为块。每次一个父块（分辨率i-1层）分为四个子块（分辨率i层）。

示意图如下:
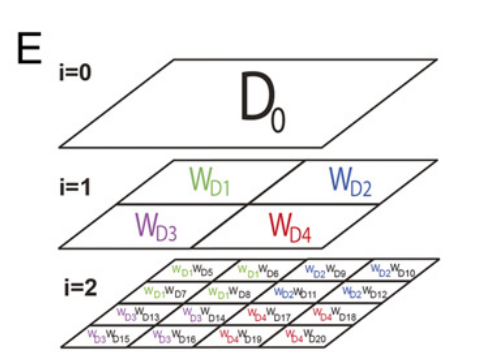
image-20211116164858893

在分辨率为i层时，一次出行走出其所在起始块的概率为

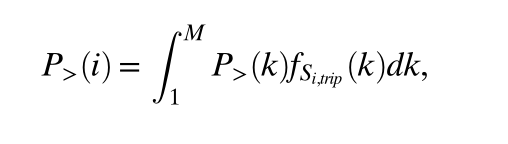
image-20211116165145462

起始块超出概率在不同块分辨率产生移动距离的分布。

其中

  • M是在整个区域中总的提供方数量(即所有可选目的地:other位置)

  • 是k个在起始块的提供方不被选择的概率，代表基于排名的地点选择机制。

  • 是在起始块内找到k个提供方的概率，代表位置的地理分布。计算方式如下:

    image-20211116173305962

    是给定D需求在分辨率水平为i从起始块移动的条件概率。是给定需求后供应的条件概率。Q是在整个研究区域中需求数。

总的来说，要通过量化移动距离,我们不仅需要每个类型位置的分布，而且需要它们在不同尺度上的相关性。

Materials and Methods相关资料:

对于给定子区域 ,是在起始的出行数，是在的出行目的地数。使用二元随机变量来代表区域中需求和提供地点数。其中X是由一个级联过程产生的，在这个过程中，不同空间尺度的波动以相乘的方式结合在一起。

在一个通用的i块中，供应和需求是和,密度相关度量为

首先在初始块均匀测量供需密度和，然后逐步将初始块划分为。在子块中的供需密度需乘以非负的随机因子和(平均值为1)，随机因子组成的向量是级联的生成器。

即使级联生成器在不同分辨率i下有独立取值，但它们的分量和在给定i中可能是互相依赖的。

在分辨率i−1和i下测量的密度关系式为

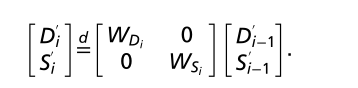
image-20211119203226257

在更小尺寸的块中，空块不能被忽略。在这种情况下，最好将生成器建模为β级联，块要么为满，要么为空。二元β级联的生成器具有一个离散分布，其概率质量集中在四个()点:

at at at at

在一个给定的区域内，用层次乘法级联分析框架来描述人口和场所设施分布的协方差，考虑了区域特定空间结构对个体出行距离的影响。

这使得我们能够对城市土地利用的变化如何影响微观层面的个人出行行为和宏观层面的OD矩阵进行情景测试。

Results

Extracted Mobility Features from Mobile Phone Data

对每个个体，直接从数据中提取，和使用时间马尔科夫模型进行标定(calibrate)。其余参数如排名选择机制的参数，偏好返回机制的参数,在全部人口的聚合数据中提取。

image-20211116174011928

该图为的联合分布。绿点为最可能的参数组合

Simulated Mobility Features

有了上述观测到的特征参数，TimeGeo模型可以在城市尺度产生长时间内个体每日移动轨迹。

以学生自愿收集的14-mo数据为例，固定家和工作地(学校)。使用模型框架来模拟灵活的Other活动的时空选择和家活动的时间选择。

计算该学生的个人参数，发现其burst rate小于人口平均水平，说明其有更小的可能性产生连续的短时间活动。

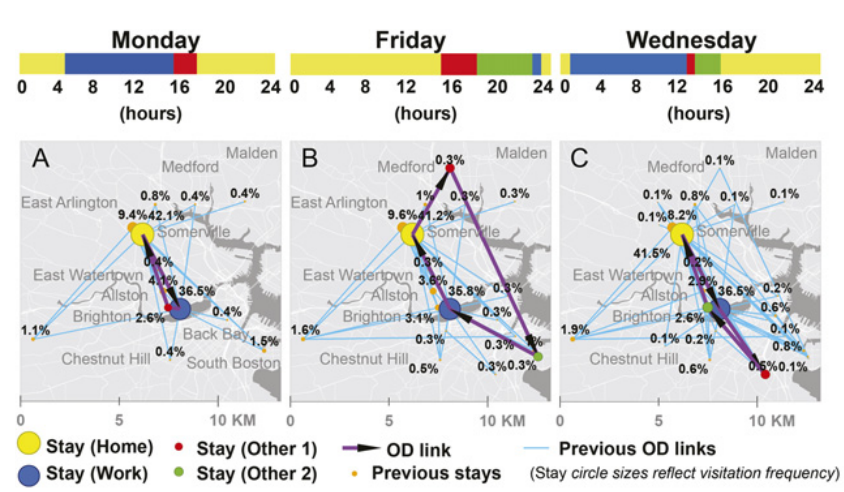
image-20211116174956650

该图为模拟该学生三天移动的结果。他每天主要在H-O(home-work)间进行移动，只有一些去Other位置的移动。该模型不仅捕捉到每天个体访问地点的数量，还捕捉了每天行程链更详细的构造。

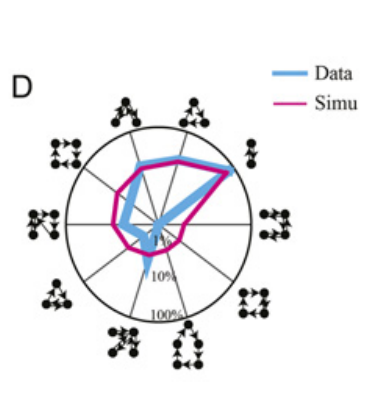
image-20211116175329672

该图展示了该学生每日移动的模体(motif)，作者使用结点代表位置，边代表位置之间发生的移动，并统计模体的分布。主导的模体是在一天中在两个位置之间移动。

TimeGeo模型的关键在于使用ICT记录产生个体移动轨迹。对于数据稀疏的个体(在30天中只有4 个不同的位置)，作者模拟他时空完整的移动轨迹:
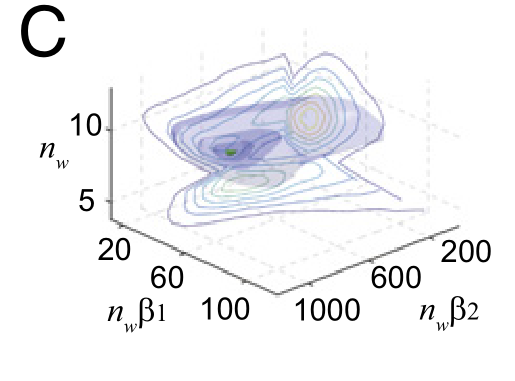
在联合分布中选择两组参数来产生这个用户的两组合成轨迹。

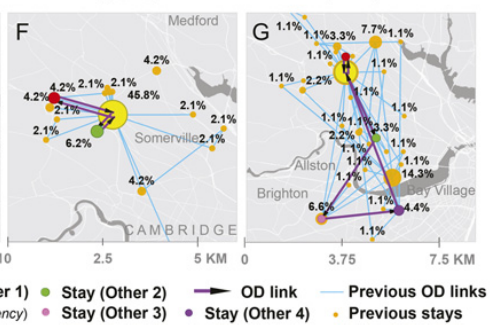
image-20211117155712292

左图使用参数

右图使用参数

较大的和产生更多连续的out-of-home活动，访问更多地点。

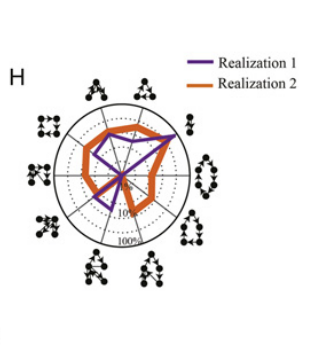
image-20211117155946701

该图展示了该用户通过这两组参数模拟的每日移动的模体，较小的参数更倾向于简单的模体，较大的参数有更复杂的活动链。

作者通过绘制三种不同参数个体(频繁移动/不太频繁移动/中值)停留时间()和访问地点数(N)的分布发现不太频繁移动的个体明显有更长的停留时间和更少的位置访问。

为了量化模型模拟和实证数据分布之间的差异,作者使用KS检验( Kolmogorov–Smirnov test)。

两种极端个体(频繁移动/不太频繁移动)实证和模拟P()的KS统计值为0.12和0.11,如果将他们的实证数据和中值个体模拟进行比较，KS值增加。同样，作者也计算了P(N)实证和模拟的KS值。这证实了包含个人特定参数来模拟时间选择的重要性。

随后作者做了类似于消融实验的分析，来证明模型中的每个机制(,r-EPR)都是至关重要的。

对于dwell rate,如果使之都为1，该模型不区分家和other活动的移动倾向，结果导致低估了短时间的出行，KS检验统计值从0.04增加至0.27。

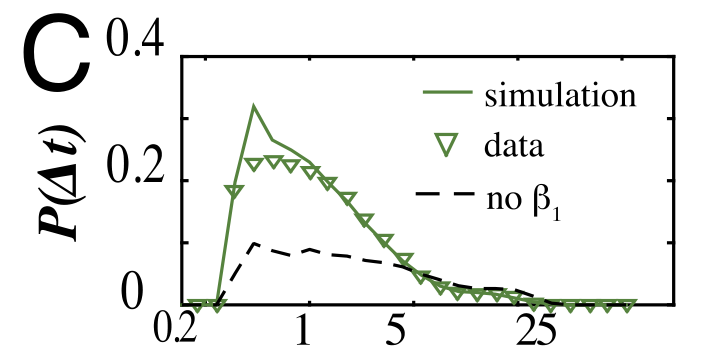
image-20211119162259558

对于burst rate，模型是否带有这个参数P(N)分布的KS统计值为0.03和0.22。

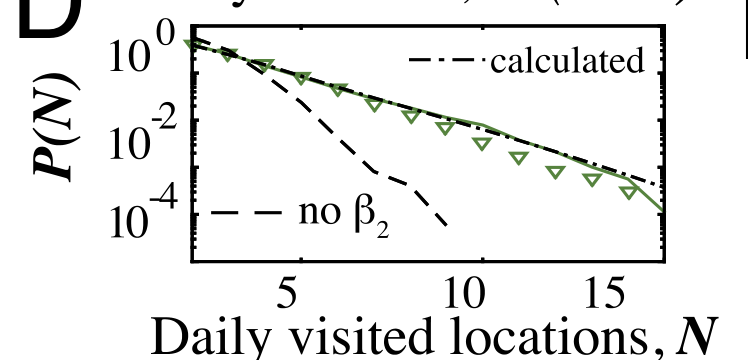
image-20211119163026348

和捕捉了灵活活动的爆发 ，来确保停留时间和访问地点的数目P(N)。

EF两图展示了有无偏好返回机制个体L-th位置访问频率对比和有无基于排名选择机制个体出行距离对比来说明机制的重要性。

作者扩展用户(通勤者和非通勤者)到人群(年龄超过16岁)，并产生一个工作日的移动轨迹。作者使用模拟产生的移动轨迹和传统出行调查数据进行对比。

分别使用MTS(一个州的出行调查)和NHTS(国家家庭出行调查)

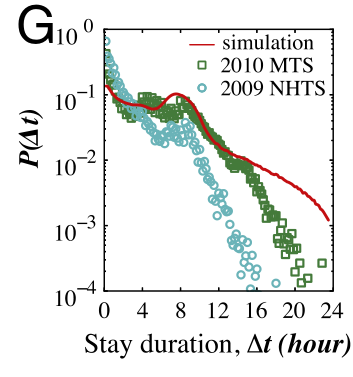
image-20211119164505567

分布的KS检验值分别为0.23和0.59。发现调查数据和模拟数据之间的停留时间分布显著不同，这主要是因为在一天的调查中人们很少报告停留时间超过12小时的活动，而模拟使用的信息由活跃的手机用户的数据记录提供。

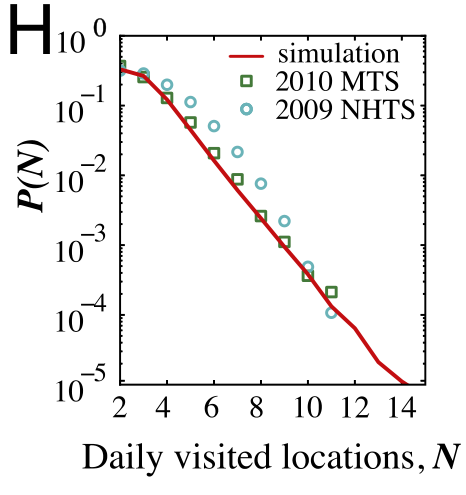
image-20211119164937417

P(N)的分布相比较好，KS检验值为0.07和0.23。

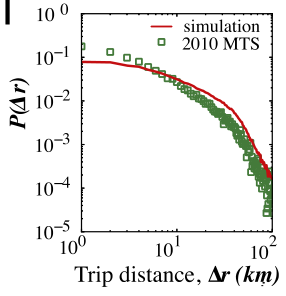
image-20211119165132169

模拟数据相比于MTS数据,KS检验值为0.24。
因为模型在选择选择返回地点时没有考虑行程距离，高估了长距离的行程。此处没有和NHTS进行比较是因为出行的空间层面取决于城市的特定扩展，在全国区域不同。

Conclusion

TimeGeo模型可以根据任何城市的人口密度和场所设施分布灵活适应到不同应用场景。最低要求是要有人口和场所设施分布。

在目前的结果中，模型的探索和返回参数()在人口中假定是相同的，个体的时间流动率假定独立于实际位置。在未来的研究中，随着更多的高频率和长时间的数据可用，有可能学习到提出参数个体层面的不同。以及在不同城市区域,不同人口结构和生活方式中模型参数的不同。

补充

Markov Chain

https://zhuanlan.zhihu.com/p/26453269

https://www.zhihu.com/question/37588564

随机过程:随机过程使用一些统计模型，利用这些统计模型可以对自然界的一些事物进行预测和处理。

马尔科夫链是随机过程的一种，每个时刻具有状态分布。每个状态的转移是有概率的，即转移概率矩阵P，且它是保持不变。有了转移概率矩阵和初始状态分布，就可以推算出后续时刻的状态分布。

马尔科夫链的状态分布只取决于现在，与过去无关。

在第n+1刻的状态只跟第n刻的状态有关,与第n-1,n-2,n-3,…等时刻的状态是没有任何关系。在随机游走的例子里，下一刻走到什么地方只与这一刻有关。

非齐次马尔科夫链模型

https://zhuanlan.zhihu.com/p/31999081

KS检验

https://www.cnblogs.com/arkenstone/p/5496761.html

https://www.cnblogs.com/jiangkejie/p/11572205.html

Kolmogorov-Smirnov是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法。

其原假设H0:两个数据分布一致或者数据符合理论分布。D=max| f(x)- g(x)|，当实际观测值D>D(n,α)则拒绝H0，否则则接受H0假设。其中D值计算两分布样本之间累积经验分布函数之差。

KS检验不需要知道数据的分布情况，可以算是一种非参数检验方法。

KS值越大，说明样本间差异越大。

  • 本文标题：The TimeGeo modeling framework for urban motility without travel surveys
  • 本文作者：y4ny4n
  • 创建时间：2021-12-25 16:01:55
  • 本文链接：https://y4ny4n.cn/2021/12/25/1102/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
此页目录
The TimeGeo modeling framework for urban motility without travel surveys
  1. Data
  2. Generating Mechanism
    1. Temporal Choices
    2. Spatial Choices
  3. Role of Land Use on Travel Distance
  4. Results
    1. Extracted Mobility Features from Mobile Phone Data
    2. Simulated Mobility Features
  5. Conclusion
  • 补充
    1. Markov Chain
    2. KS检验