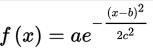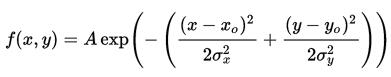SSIM(Structural SIMilarity)

SSIM( Structural SIMilarity)即图像质量评估的多尺度结构相似方法

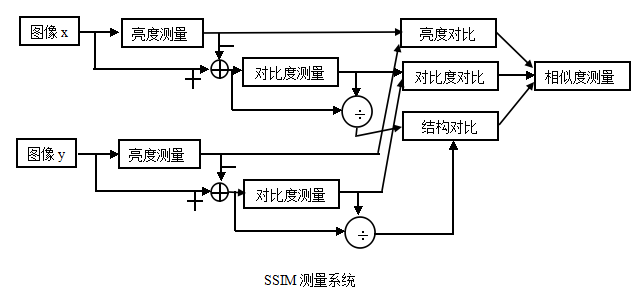
结构相似性，一种全参考的图像质量评价指标，它分别从亮度、对比度、结构三方面度量两幅图像相似性。

图源:https://github.com/Po-Hsun-Su/pytorch-ssim

paper:https://www.researchgate.net/publication/4071876_Multiscale_structural_similarity_for_image_quality_assessment

Abstract

该评估方法基于假定人的视觉系统高度适应于提取场景中结构信息，因此该方法可以提供一个很好的近似来感知图片质量。论文中提出一种图像合成方法来标定定义不同尺度相关重要性的参数。

Intro

使用最广泛的全参考图像质量和失真评估算法是峰值信噪比(PSNR)和均方误差(MSE)，它们与图像感知质量的相关性并不好。

传统的感知图像质量评估方法是基于自底向上的方法，试图模拟相关的早期人类视觉系统(HVS)组件的功能。这些方法通常包括

1)一个可能包含图片对齐，点向的非线性变换，模拟人眼光学的低通滤波，和颜色空间转换的预处理过程。

2)信道分解过程，把图像信号转换为不同的空间频率以及方向选择子带

3)误差归一化过程，通过合并综合在不同子带中视觉灵敏度变化以及由通道内或通道间相邻变换系数引起的视觉误差灵敏度的变化对每个子带的误差信号进行加权。

….看不下去了

SINGLE-SCALE STRUCTURAL SIMILARITY

单一尺度结构相似

为方差 为方差 为x和y的协方差

近似可以把和看成是亮度和对比度的估计， 测量了x和y一起的变化形势。论文中给出了亮度、对比度、结构相似测量:

c1,c2,c3为常数

L为像素值的动态范围(对于8位/像素灰度图像，L = 255) K1<<1 K2<<1 是两个标量常数

SSIM的通式被定义为:

我们一般设定

故得到，并且遵守

1)对称性 SSIM(x,y)=SSIM(y,x)

2)有界性 SSIM(x,y)1

3)独有的最大值 只有x=y时, SSIM(x,y)=1

通用图像指标适用于C~1~=C~2~=0的情况，这样进行参数设置的缺点是当SSIM通式中分母接近0时，测量结果变得不稳定。添加两个小常量C~1~和C~2~使这个问题很好解决(由K~1~=0.01和K~2~=0.03分别计算得到)。

我们将SSIM索引算法应用于图像质量的滑动窗口评估，窗口在整个图像空间逐像素移动。每一步，SSIM索引在当前窗口内计算。

如果被比较的其中一幅图像被认为具有完美的质量，那么得到的SSIM索引图可以被视为另一幅(失真的)图像的质量图。

不像在[3]中那样使用8 × 8的正方形窗口，平滑窗口方法用于当前统计，以避免在质量图中出现“blocking artifacts”

最后，利用质量图的均值SSIM对图像的整体质量进行评价。

MULTI-SCALE STRUCTURAL SIMILARITY

多尺度结构相似

Multi-scale SSIM index

图像细节的可感知性取决于图像信号的采样密度，图像平面到观测者的距离以及观测者视觉系统的感知能力。当这些因素不同时，对给定图像的主观评估也会不同。上一部分描述的单一尺度方法可能只适用于特定设置。多尺度方法是一种便利的方法来整合不同分辨率的图像细节。

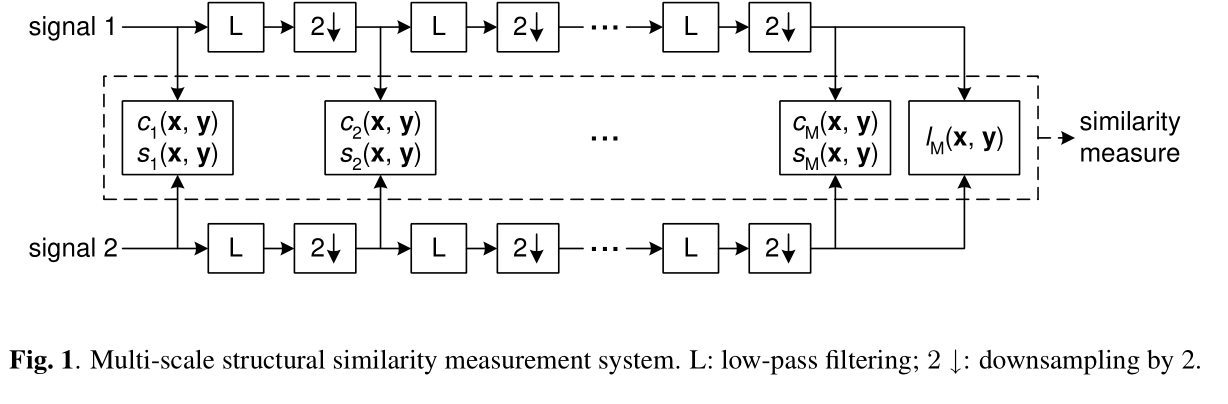
以参考图像和失真图像信号作为输入，迭代地应用低通滤波器并对滤波后的图像进行2倍的下采样。规定原始图像为Scale 1,最后输出的图像为Scale M,进行了M-1次迭代。在第j个尺度，对比度和结构对比计算为和。亮度对比只在Scale M计算。

SSIM是将不同尺度的测量结果结合起来得到的

同样用来调整不同部分的相对重要性

为了简化参数选择，我们对所有j设置

另外标准化跨尺度设置

这使所有不同参数设置(包含所有单尺度和多尺度的设置)具有可比性

接下来设置不同尺度的相关值

概念上说这个应该和人类视觉系统(HVS)的对比敏感度函数相关(CSF),CSF函数表明人类视觉敏感度在中频处达到峰值(每度视觉角度约4个周期)，沿高、低频方向均有所下降。然而CSF不能直接用于推导我们的参数，它通常是在可见阈值水平上使用简化刺激(正弦)测量的(?说啥呢)，但我们的目的是比较在可见失真水平下复杂结构图像的质量。

Cross-scale calibration

我们使用图像合成方法来标定不同尺度的相对重要性

MSE: https://blog.csdn.net/qq_38701868/article/details/99703998

数理统计中均方误差是指参数估计值与参数真值之差平方的期望值，记为MSE。MSE是衡量“平均误差”的一种较方便的方法，MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。

论文中给出对于一张给定8位/像素灰度测试图像，进行合成的失真图像表。

每张失真图像通过迭代过程生成，初始图像随机添加了高斯白噪音，迭代的过程使用了约束梯度下降方法(constrained gradient descent)在SSIM测量下寻找最坏图像，同时约束MSE是固定的，并限制失真仅在指定的尺度内发生。

实验中使用了5个尺度和12个失真等级，即使每行图片具有相同的MSE，它们的视觉质量也是很明显不同的，所以失真在不同尺度有很大差异。

实验使用了10张不同类型内容的图像(人脸，自然景观，植物，人造物品..)并创建10组失真图像。收集了八名受试者的数据，每名受试者一次看到一组测试图像，视野距离限制在每度视角32像素。受试者需要比较不同尺度的图片质量，并从每个尺度中选择认为具有相同质量的图像。例如，一个受试者选择了上图中圈出的认为具有相同质量的图像，记录在每个尺度被选择图片的位置并对所有测试图像和受试者进行平均计算。总的来说，受试者互相同意相比于自己选择的图像更多。

这些测试结果被标准化并用于计算前面式子中提到的相关指数。结果参数为:

补充

看完论文后看代码 wc… 不能说一模一样 简直是毫不相关

又面向百度补充了一些数学芝士以及相关代码

为什么使用均值/标准差/协方差

https://zhuanlan.zhihu.com/p/93649342

用均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的度量。

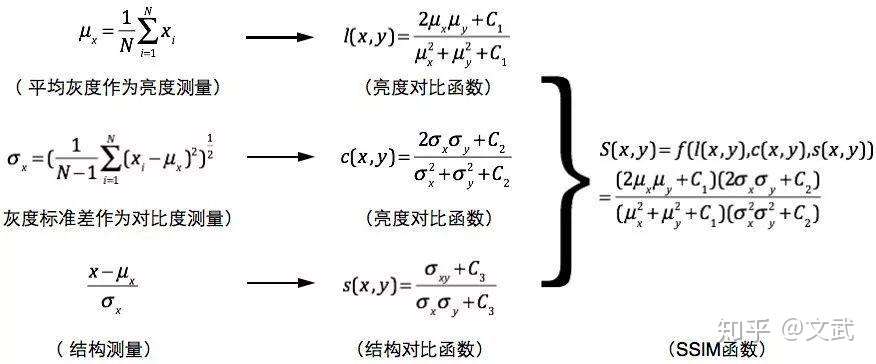
https://blog.csdn.net/qq_36387683/article/details/108048693

把与物体结构相关的亮度和对比度作为图像中结构信息的定义。因为一个场景中的亮度和对比度总是在变化的，所以我们可以通过分别对局部的处理来得到更精确的结果。

高斯函数

https://blog.csdn.net/qinglongzhan/article/details/82348153

一维

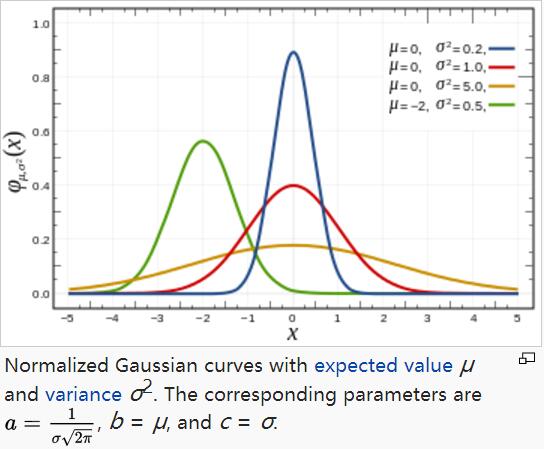
高斯函数广泛应用于统计学领域，用于表述正态分布，在信号处理领域，用于定义高斯滤波器，在图像处理领域，二维高斯核函数常用于高斯模糊Gaussian Blur。

高斯的一维图是特征对称“bell curve”形状，a是曲线尖峰的高度，b是尖峰中心的坐标，c称为标准方差，表征的是bell钟状的宽度。

二维

A是幅值，x~0~ y~0~是中心点坐标，σx σy是方差

以(0,0)为中心点

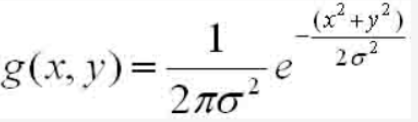
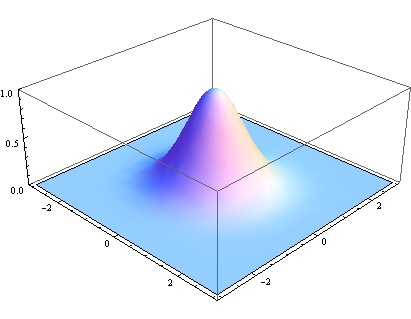
高斯模糊

http://www.ruanyifeng.com/blog/2012/11/gaussian_blur.html

高斯模糊将正态分布(高斯分布)用于图像处理，它是一种数据平滑技术 （data smoothing）

原理

所谓”模糊”，可以理解成每一个像素都取周边像素的平均值。

“中间点”取”周围点”的平均值，就会变成1。在数值上，这是一种”平滑化”。在图形上，就相当于产生”模糊”效果，”中间点”失去细节。

图见引用链接

计算平均值时，取值范围越大，”模糊效果”越强烈。

如果使用简单平均，显然不是很合理，因为图像都是连续的，越靠近的点关系越密切，越远离的点关系越疏远。因此，加权平均更合理，距离越近的点权重越大，距离越远的点权重越小。

权重

正态分布是一种可取的权重分配模式。

在图形上，正态分布是一种钟形曲线，越接近中心，取值越大，越远离中心，取值越小。

计算平均值的时候，我们只需要将”中心点”作为原点，其他点按照其在正态曲线上的位置，分配权重，就可以得到一个加权平均值。

有了高斯函数，我们可以计算每个点权重。

权重矩阵与计算

计算细节见链接，写的很清楚。

为了计算权重矩阵，需要设定σ的值。

需要让周围点的权重之和等于1。

对所有点重复这个过程，就得到了高斯模糊后的图像。如果原图是彩色图片，可以对RGB三个通道分别做高斯模糊。

高斯核与卷积

https://blog.csdn.net/weixin_39124778/article/details/78411314

卷积可以帮助实现平滑算法。

有噪点的原图，可以把它转为一个矩阵：

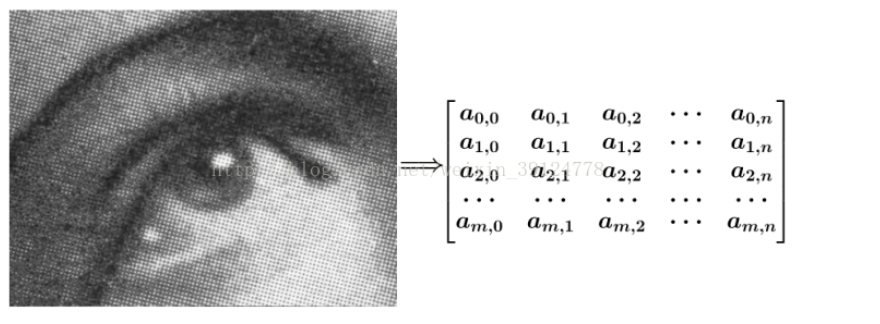
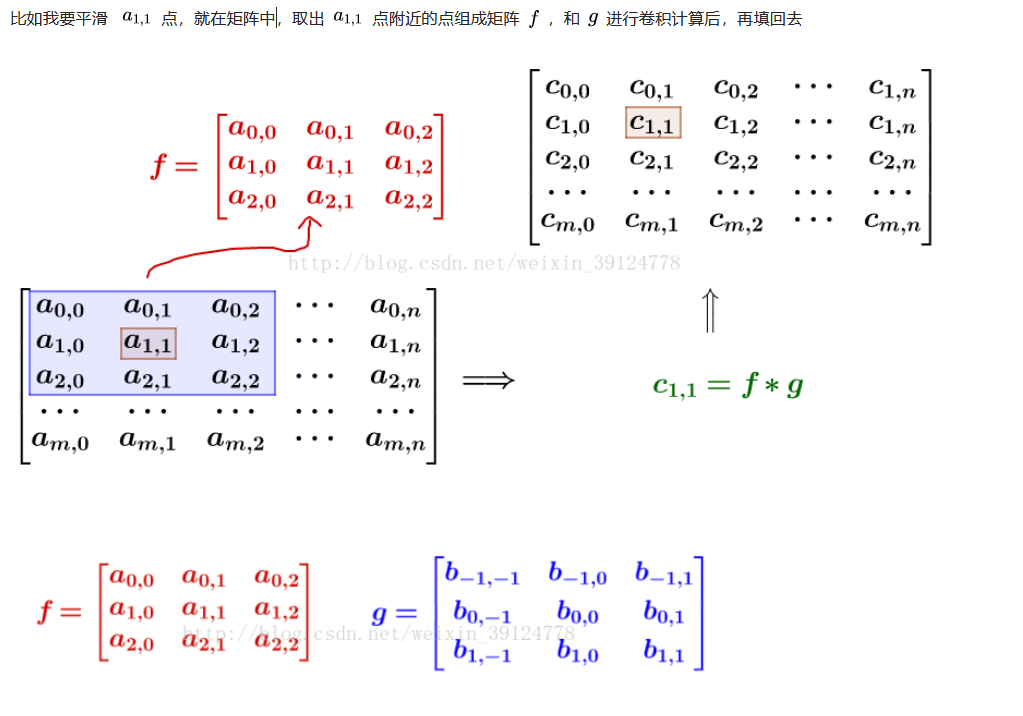
在图像平滑处理时，函数g通常取高斯核函数(高斯核函数的由来可以参考上面高斯模糊链接中的过程)。

高斯核函数关于中心对称，所以直接对应相乘与旋转180°相乘效果一样

这样相当于实现了g矩阵在原来图像上的划动

生成高斯核

https://blog.csdn.net/qq_16013649/article/details/78784791

通过一维生成二维

由于高斯滤波器是可分的(G(x,y)=G(x)*G(y))，所以可以用一维高斯核得到二维高斯核

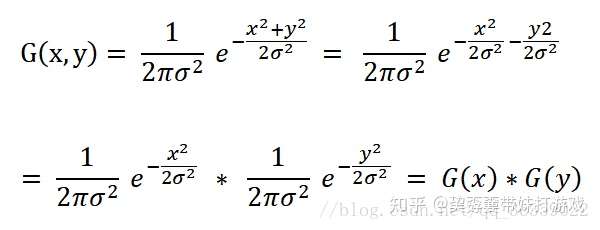
先获取两个一维高斯核，而后对后一个高斯核进行转置，而后第一个高斯核和第二个高斯核通过矩阵相乘就可以得到一个二维高斯核了。

直接生成二维

for i in range(gaussian_kernel_width):
    for j in range(gaussian_kernel_width):
        gaussian_kernel[i,j]=\
        (1/(2*pi*(gaussian_kernel_sigma**2)))*\
        exp(-(((i-5)**2)+((j-5)**2))/(2*(gaussian_kernel_sigma**2)))

计算细节

https://blog.csdn.net/qq_36387683/article/details/108048693

在实际应用中，一般采用高斯函数计算图像的均值、方差以及协方差，而不是采用遍历像素点的方式，以换来更高的效率。

在上述公式中，都加入了一个8*8的方形窗，并且逐像素的遍历整幅图片。每一步计算，和SSIM都是基于窗口内像素的，最终得到一个SSIM指数映射矩阵，由局部SSIM指数组成。然而，简单的加窗会使映射矩阵出现不良的“分块”效应。作者实际上采用σ=1.5的高斯加权函数计算每个图像块(图像块大小11x11)的均值和标准差。

边界点的处理

如果一个点处于边界，周边没有足够的点

代码中采用的处理方式是padding=window_size//2

低通滤波

https://www.cnblogs.com/luyaoblog/p/7160948.html

代码

生成一维高斯核

def gaussian(window_size, sigma): #生成一维高斯核
    gauss = torch.Tensor([exp(-(x - window_size//2)**2/float(2*sigma**2)) for x in range(window_size)])
    return gauss/gauss.sum()#归一化

生成二维高斯核

def create_window(window_size, channel):#通过一维高斯核生成二维
    _1D_window = gaussian(window_size, 1.5).unsqueeze(1)#升维
    _2D_window = _1D_window.mm(_1D_window.t()).float().unsqueeze(0).unsqueeze(0)
    window = Variable(_2D_window.expand(channel, 1, window_size, window_size).contiguous())
    #expand参数中 第一个参数是输出通道 即卷积核数量，输出通道数=channel说明经过卷积后通道数不变
    #第二个参数是inchannel(输入通道,与输入图像相同的通道数)/groups,由于groups=channel,所以在这里等于1

    return window

计算SSIM

def _ssim(img1, img2, window, window_size, channel, size_average = True):
    mu1 = F.conv2d(img1, window, padding = window_size//2, groups = channel) #卷积求均值
    mu2 = F.conv2d(img2, window, padding = window_size//2, groups = channel)

    mu1_sq = mu1.pow(2)
    mu2_sq = mu2.pow(2)
    mu1_mu2 = mu1*mu2
    # 在计算方差和协方差时用到了公式Var(X)=E[X^2]-E[X]^2, cov(X,Y)=E[XY]-E[X]E[Y].(这块盯了好久没懂，后来看到这个公式...还是太拉了
    sigma1_sq = F.conv2d(img1*img1, window, padding = window_size//2, groups = channel) - mu1_sq #求方差
    sigma2_sq = F.conv2d(img2*img2, window, padding = window_size//2, groups = channel) - mu2_sq
    sigma12 = F.conv2d(img1*img2, window, padding = window_size//2, groups = channel) - mu1_mu2  #求协方差

    C1 = 0.01**2
    C2 = 0.03**2

    ssim_map = ((2*mu1_mu2 + C1)*(2*sigma12 + C2))/((mu1_sq + mu2_sq + C1)*(sigma1_sq + sigma2_sq + C2))

    if size_average:
        return ssim_map.mean()
    else:
        return ssim_map.mean(1).mean(1).mean(1)
    	#不是太理解，留坑

定义类

class SSIM(torch.nn.Module):
    def __init__(self, window_size = 11, size_average = True):
        super(SSIM, self).__init__()
        self.window_size = window_size 
        self.size_average = size_average
        self.channel = 1 
        self.window = create_window(window_size, self.channel) #用初始化的channel创建window

    def forward(self, img1, img2):
        (_, channel, _, _) = img1.size()#取img1的通道数

        if channel == self.channel and self.window.data.type() == img1.data.type():#判断初始化通道与img1通道数 判断window的数据类型与img1数据类型
            window = self.window
        else:
            window = create_window(self.window_size, channel) #若不相等，创建img1 channel的window
 
            if img1.is_cuda:
                window = window.cuda(img1.get_device())
            window = window.type_as(img1) #将window的数据类型转换为与img1相同

            self.window = window #使用通过img channel创建的window
            self.channel = channel #使用img1 channel


        return _ssim(img1, img2, window, self.window_size, channel, self.size_average)

感觉定义类中输出输入的通道数和Conv2d中传入的高斯核window的中的参数有点绕

代码理解参考:

https://blog.csdn.net/qq_17457331/article/details/88044462

https://jianzhuwang.blog.csdn.net/article/details/106450239

https://blog.csdn.net/demo_jie/article/details/107197809

代码注释和论文解读可能有错，凑合着看TnT