基于深度蒙特卡洛的斗地主研究

在完成毕业论文期间入门了解RL理论知识的笔记。

RL相关

基本概念

专业术语

• state (this frame) action

  智能体当前的情况。智能体做出行为前后智能体所处的环境，即对当前时刻环境的概括。

• policy

  根据观测到的状态做出决策控制agent做出动作

  该概率密度函数表示给定状态做出动作的概率，exp:

  policy根据概率进行随机抽样:以0.2向右，0.1向左，0.7向上。三种动作都有可能发生，但向上的概率最大。

• reward

  在智能体执行一个动作之后，环境返回给智能体的一个数值。奖励定义得好坏非常影响强化学习的结果。奖励值可正可负。

• state transition

  old state —-action——> new state

  通常认为状态转移是随机的(马尔科夫链)，状态转移的随机性来源于environment(游戏程序)。

  exp: P(goomba left)=0.8 P(goomba right)=0.2

  状态转移函数只有环境知道，玩家不知道。

• agent environment interaction

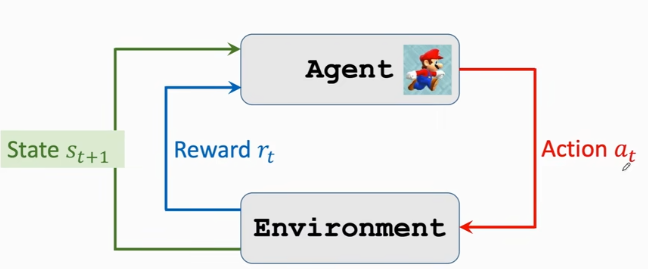
在每个时刻t，智能体观测到环境的状态s，做出动作 a，动作会改变环境的状态，环境反馈给智能体奖励 r 以及根据状态转移函数产生新的状态 s ′ 。此过程将继续进行，直到智能体达到终端状态，即走完一整个回合(episodes)。回报是折现后的累积奖励，智能体的目标是最大化每个状态对这种长期回报的期望。

• RL随机性的来源

  action具有随机性。 根据policy随机抽样得到

  状态转移具有随机性。 给定状态s和动作a，环境随机抽样产生新的状态s’

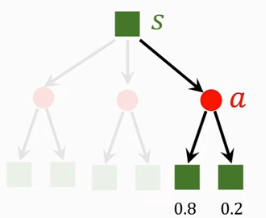
• trajectory(state,action,reward):
  oberseve state,make action,environment gives and reward

• rewards and returns

  • return(回报/cumulative future reward)

  • Discounted return(discounted cumulative future reward

    折扣率为超参数

    未来的价值随着时间的加长变得越来越廉价，因为存在风险。agent在当前的state下的价值就是未来所有可能reward的折现到此时此刻的价值。这么考虑就可以让agent去关注到未来可能存在的reward，但是更加关注当前的reward，因为时间越长，对未来的预测越不准。

    折扣率接近于0时，agent更在意短期回报；越接近于1时，长期回报变得更重要。

    对任意大于t的时刻i,reward 都取决于 和.给定，随机变量return取决于随机变量:

• value function

  • action-value function动作价值函数

    函数为对未来所有奖励的期望

    为未来所有状态和动作的函数，未来的动作和函数都具有随机性

    Action:

    state:

    对求期望E把这些随机变量积掉从而排除中的随机性，与当前动作和状态，policy有关。

    动作价值函数直观意义：如果用policy，在状态下，做动作是好还是坏

    已知policy ，就会给当前状态下所有动作打分，分辨动作好与不好。不同policy，不同。

    For policy， evaluates how good it is for an agent to pick action a while being in state s.

    最优动作价值函数(去掉,使用最好的policy函数，使得最大化)

    只与当前动作和状态有关，agent可以根据当前状态对动作的评价来做决策

    Whatever policy function is used,the result of taking at state cannot be better than

  • state-value function状态价值函数

    动作为离散变量

    动作为连续变量(例如自动驾驶中方向盘旋转度数)

    把动作A看作随机变量，关于动作A求期望，把A消掉。只与状态s有关。

    状态价值函数直观意义: 评价当前状况好坏，快赢了还是快输了

    For policy， evaluates how good the situation is in state s.

    若固定，则状态s越好，数值越大。

    还能评价policy的好坏，越好， 越大。(的平均值)

• 两种学习方式/目标

  • 策略学习 得到

    每观测到状态，算出概率密度函数，随机抽样做出动作

    在基于策略的强化学习方法中，智能体会制定一套动作策略（确定在给定状态下需要采取何种动作），并根据这个策略进行操作。强化学习算法直接对策略进行优化，使制定的策略能够获得最大的奖励。

  • 价值学习 得到

    每观测到状态,把作为输入，使对每个动作做出评价，选出 值最大的动作s

    在基于价值的强化学习方法中，智能体不需要制定显式的策略，它维护一个价值表格或价值函数，并通过这个价值表格或价值函数来选取价值最大的动作。

  • 应用场景

    基于价值迭代的方法只能应用在不连续的、离散的环境下（如围棋或某些游戏领域），对于动作集合规模庞大、动作连续的场景（如机器人控制领域），其很难学习到较好的结果（此时基于策略迭代的方法能够根据设定的策略来选择连续的动作）。

    基于价值的强化学习算法有Q学习（Q-learning）、 Sarsa 等，而基于策略的强化学习算法有策略梯度（Policy Gradient，PG）算法等。

    此外，演员-评论员算法同时使用策略和价值评估来做出决策。其中，智能体会根据策略做出动作，而价值函数会对做出的动作给出价值，这样可以在原有的策略梯度算法的基础上加速学习过程，取得更好的效果。

• episode

  对于一个有限游戏，一次游戏称为一个episode(回合)，就是指这一个回合的终极目标，比如说，一局棋的胜负，一场拳击比赛的胜负，一场战役的胜负。

  假定智能体与环境的交互存在一个最终时间步，其对应的状态称之为最终状态。以一个最终状态为结束标志的智能体与环境的交互序列我们称之为一个回合(episode).比如说，一场比赛、一局棋、一次迷宫挑战等等。每个回合结束后会得到不同的结果，对应着不同的回报。这种具有回合特征的任务我们称之为回合制任务(episodic tasks)。

  在有些情况下，一个任务没有明确的最终状态，而是无限地延申下去。比如说一个机器人在其生命期内的学习过程，或者我们自己终其一生的学习和成长过程。这种任务我们称之为连续性任务（continuing tasks）。

  有的强化学习算法如TRPO是用整个episode的数据一起拿来训练的，有的算法如DDPG则是agent的每步step的数据都可以训练。

  连续性任务与回合制任务区别

  https://chenxiaoyuan.blog.csdn.net/article/details/122457558

OPEN AI Gym

经典控制问题 Cart Pole/Pendulum

import gym
env=gym.make('CartPole-v0')

Atari Games Pong/Space Invader/Breakout

连续控制问题MuJoCo 控制Ant/humanoid移动

state=env.reset()
for t in range(100):
    env.render() #A window pops up rendering CartPole
    action=env.action_space.sample() #A random action.实际上动作需要通过Policy函数或Q函数得出，而非随机抽样。此时得到动作但并没有实际做出。
    state,reward,done,info=env.step(action) #做出动作，并返回当前state,reward
    if done: #done=1 means finished(win or lose the game)
        print('Finished')
        break
env.close()   

价值学习

Deep Q-Network(DQN)

使用神经网络近似Q函数

类似于先知，预见未来的结果 。可以告诉每个动作的平均回报，agent根据做决策选择平均回报最高的动作。

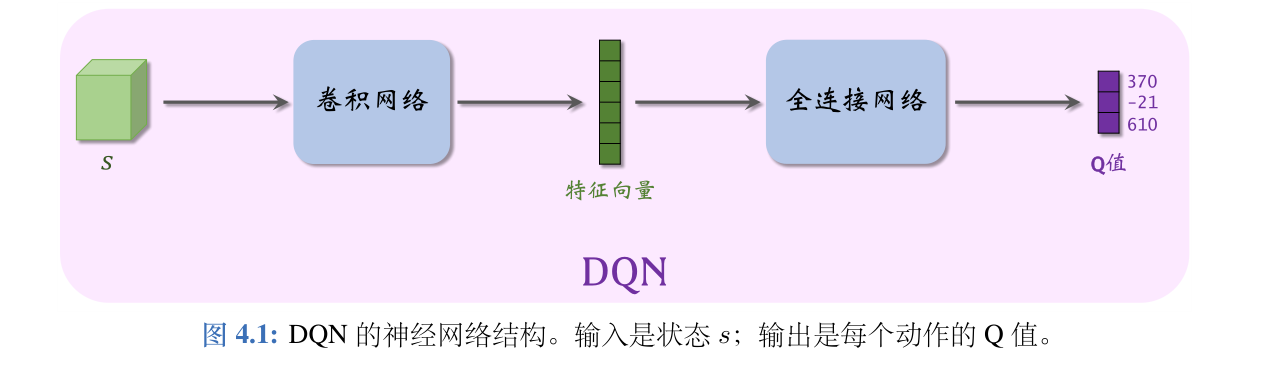
价值学习的基本想法是学习一个函数来近似

使用神经网络来近似

神经网络输入为状态s,输出为对所有可能动作的打分，每个动作对应一个分数。通过奖励学习神经网络，则神经网络给动作的打分会逐渐改进，打分越来越准。

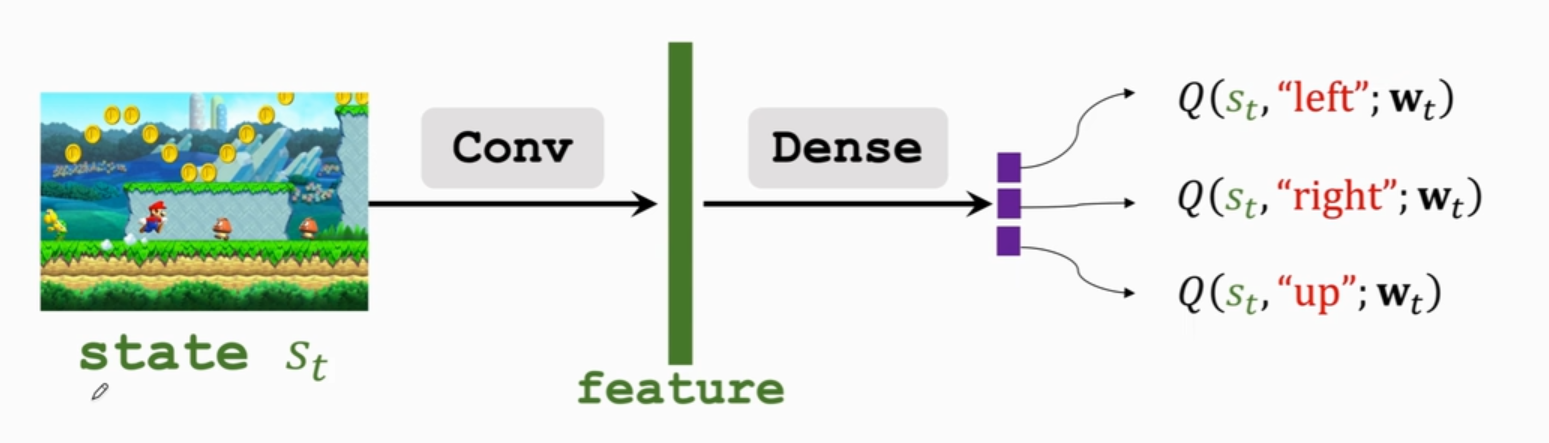
将画面作为输入，用卷积层把图片变成特征向量，用全连接层把特征映射到输出向量。输出向量为对动作的打分。

Temporal Difference(TD) Learning

使用模型进行预测

为模型预测值 为实际值target

Loss：

grad:

梯度下降:

但梯度下降完成参数更新需要全程走完

使用TD算法使得不完成全程也可以更新参数

时间差分算法(TD)

TD target为加入事实成分(实际观测)后的预测值，比最初纯粹的估计值q更可靠

TD 误差 δ 就是模型估计与真实观测之差

TD 算法的目的是通过更新参数 w 使得损失 减小。

策略学习

策略学习的意思是通过求解一个优化问题，学出最优策略函数或它的近似函数。

蒙特卡洛

https://blog.csdn.net/keypig_zz/article/details/124538163

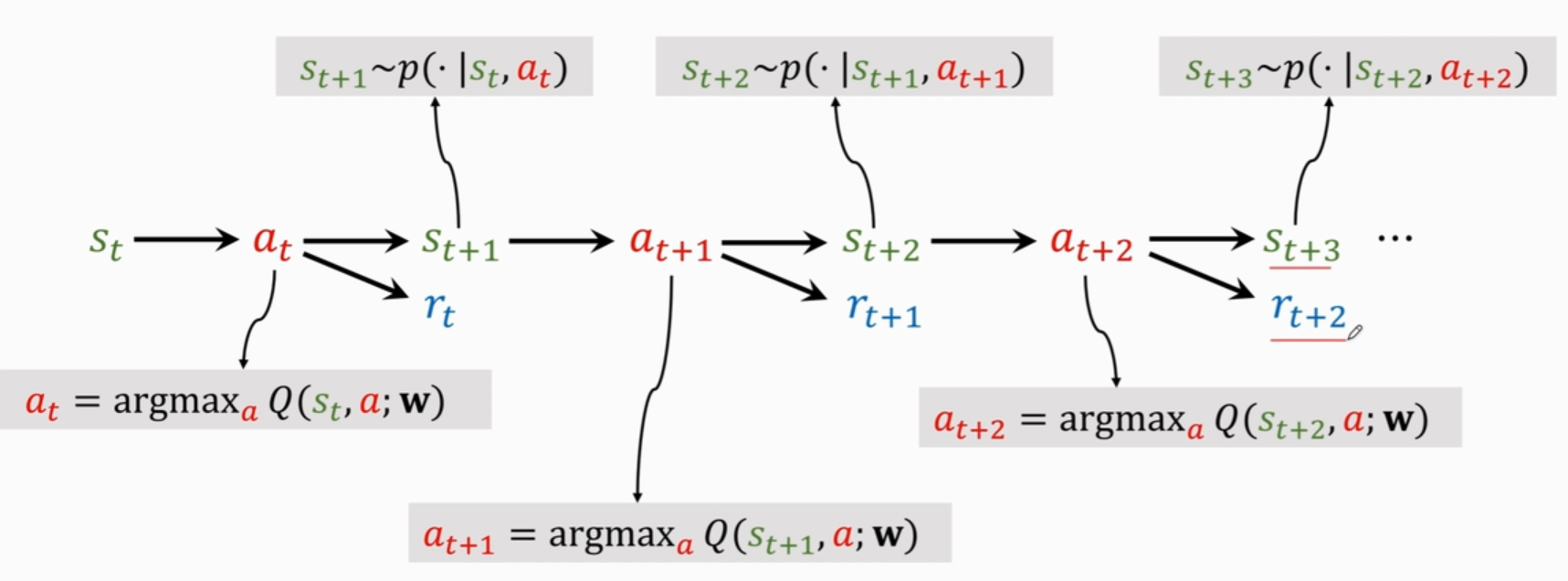
2.1.2 ϵ-greedy 策略

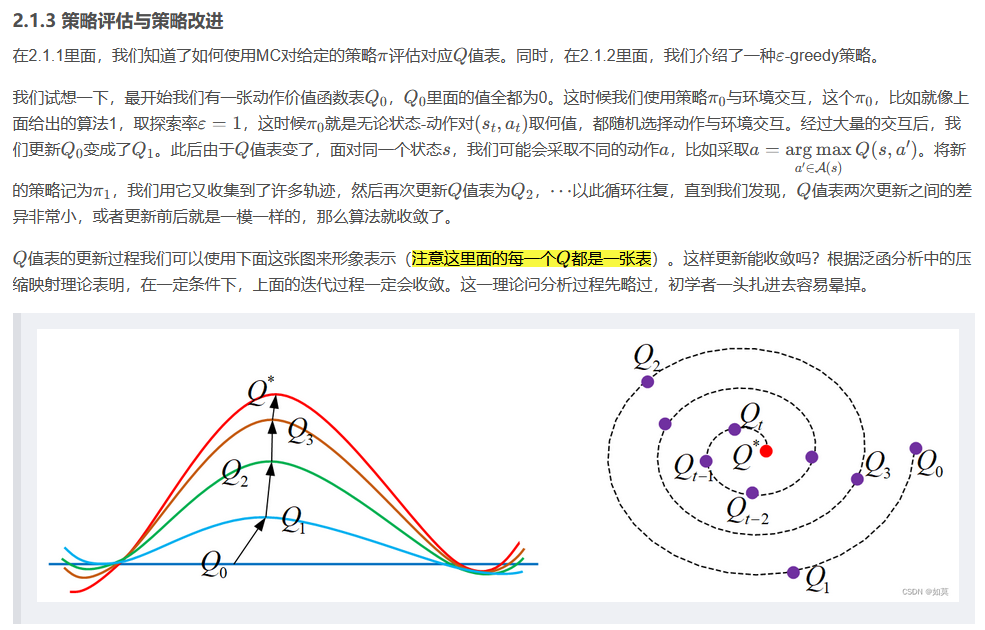
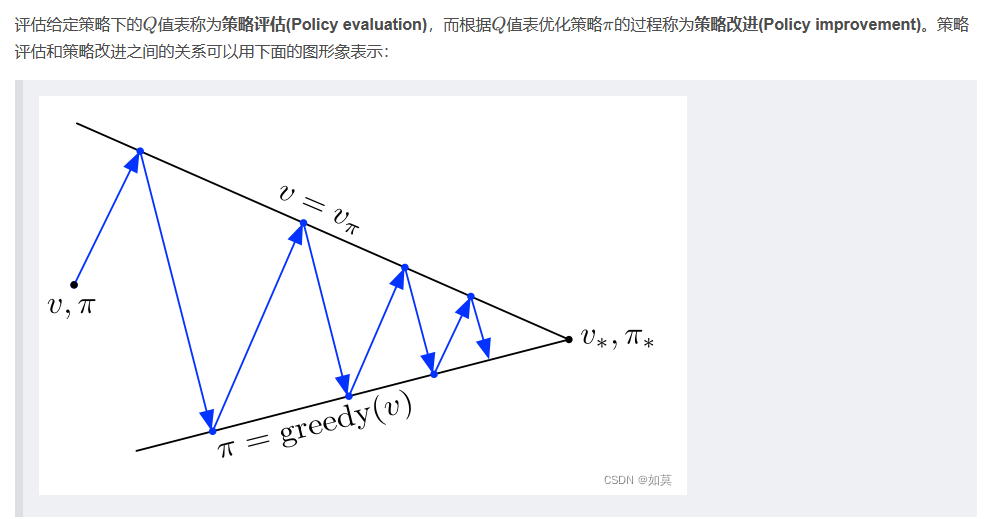
基于深度蒙特卡洛的斗地主模型

深度蒙特卡洛算法

蒙特卡洛方法为回合制的任务设计，实验可以被划分为多个回合(episode)并且所有回合最终都会终止。

蒙特卡洛方法通过样本的平均回报来估计价值函数，而不需要知道环境是如何转移的，只要经验数据即可学习。

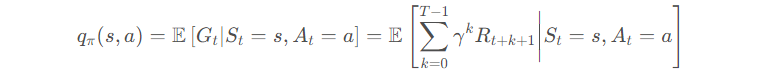
由于不知道状态转移函数P无法求出期望，需要对价值函数进行估计。

动作价值函数中包含求期望操作E，接下来我们使用蒙特卡洛的方式来替代它。

MC方法就是反复多次试验，求取每个实验中每个给定状态对的动作价值函数，即累积回报期望，然后利用均值求和求出估计值，然后得出策略评估的结果。

假设我们使用策略获得了N条状态和动作为(s,a)的轨迹，用这N条轨迹的累积奖励和的均值作为动作价值函数的一个估计，用表示:

其中表示第i条轨迹的回报。根据大数定律，只要轨迹数量足够多，且完全覆盖所有可能的轨迹，那么对估计是无偏的。

一个episode中状态-动作对(s,a)可能出现多次，我们考虑每次状态对出现都对回报进行计算(every-visit)。

为了优化策略，every-visit MC可通过迭代执行以下步骤来估计Q值表

1.按照S×A的规模生成动作价值表Q，并全初始化为0

2.使用策略与环境交互产生一个回合，生成完整轨迹

3.对在该回合中出现的每对状态对(s,a)计算并用所有样本s,a的平均回报更新Q(s,a)

4.对每个回合中的状态s，采取Q(s,a)中Q值最大的动作更新到策略中进行策略改进

在策略与环境交互生成轨迹的过程中，我们可以使用 epsilon-greedy（ ϵ-greedy）来平衡探索与利用。

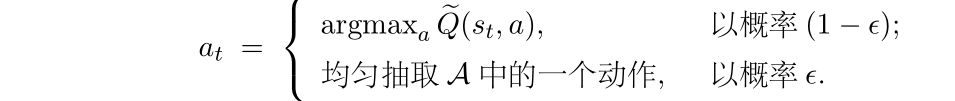
设探索率为，以概率ϵ从所有可采取的动作中随机挑选一个。否则，按照贪婪策略选择动作。

该过程可以与深度神经网络自然结合，从而形成深度蒙特卡洛(deep Monte-Carlo, DMC)。具体来说，我们可以用神经网络(DNN)代替Q表，并通过计算均方误差(MSE)替代求状态动作对的平均累积回报来更新Q网络。

该算法的基本思想是，在每个时间步，使用 策略与环境交互，并通过AI自我博弈来生成大量的轨迹。这些轨迹可以用来训练一个 DNN，以估计在当前状态下执行每个行动的价值函数（即给定当前状态，执行该行动可能导致的总收益）。这些动作价值函数估计可以直接用于指导策略，同时还可以通过改进模拟步骤中的动作选择来改善行动质量。

DouZero模型架构

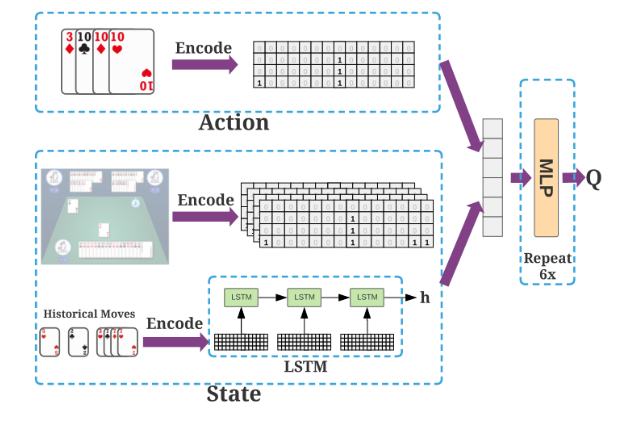
Q值网络的架构包含对历史移动进行编码的LSTM层和6层隐藏维数为512的MLP多层感知机。该网络的输入是状态和动作的串联表示，其根据该输入来预测给定状态-动作对的Q值。该网络的动作输入使用大小为54的一维向量来编码可以做出的合法动作。

该网络的状态输入提取几个卡牌矩阵来分别代表地主和农民的状态特征。其中都包含手牌矩阵、其他两名玩家手牌矩阵的合集、最近移动的卡牌矩阵、其他两名玩家已打出的手牌矩阵、最近15次移动的级联矩阵。除了卡牌矩阵之外，我们还使用一维向量来表示另外两名玩家当前的手牌和目前为止的打出的炸弹数。使用大小为17的向量表示农民的手牌，使用大小为20的向量表示地主的手牌。同样地，我们用一个15维的向量来表示当前状态下的炸弹数量。因为需要考虑两名农民之间的协作而地主只需自己获胜，农民模型需额外包含地主和另一名农民最近移动的状态特征。

我们需要将最近15次移动的级联矩阵输入到LSTM层。考虑最近的15个移动，并连接每三个连续移动的表示，即历史移动被编码到一个5 × 162矩阵中，一次移动是1x54,三次级联1x162,五个三次为5x162。使用最后一个隐藏单元来表示历史移动，并将其与上述其他的状态特征拼接作为状态输入。

当我们需要根据模型做出出牌决策时，首先将15次历史移动输入到LSTM网络中输出时序信息，再结合当前环境的状态特征与合法范围的出牌动作进行输入。输入到更新权值后的MLP，进行前向传播返回各合法动作的Q值。agent根据其给每个动作的打分进行决策出牌。